2020. 2. 2. 22:01ㆍnlp
https://towardsdatascience.com/machine-learning-basics-part-1-a36d38c7916
Machine Learning —Fundamentals
Basic theory underlying the field of Machine Learning
towardsdatascience.com
머신러닝의 유형
1. 감독학습 Supervised Learning
1.1. 분류 Classification → Logistic Regression (반응변수 y가 이산discrete)
1.2. 회귀 Regression → Linear Regression (반응변수 y가 연속continuous)
2. 무감독학습 Unsupervised Learning
3. 강화학습 Reinforcement Learning
Linear Regression
- y_hat = Wx + b
- 오차 계산
1) MAE(Mean Absolute Error)
2) MSE(Mean Squared Error)
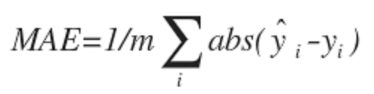
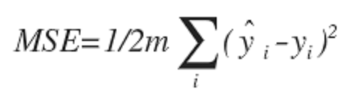
Gradient descent Algorithm
- Cost function(오차 함수)의 최솟값 찾기
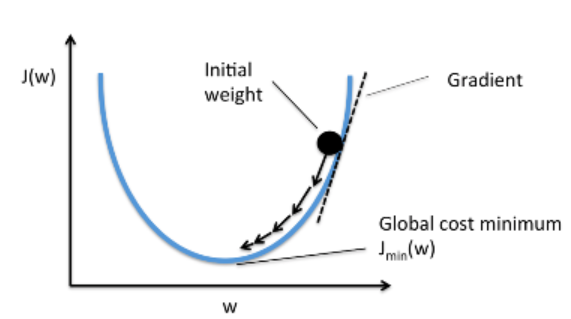
- 가중치 업데이트

- 방법 3가지
1) Batch Gradient Descent : 모든 데이터로 학습 후 가중치 업데이트
2) Mini-batch Gradient Descent : 데이터 중 일부만 학습 후 가중치 업데이트
3) Stochastic Gradient Descent (SGD) : 데이터 한 개만 학습 후 가중치 업데이트
* 이 데이터가 랜덤하게 선택되기 때문에 'stochastic 확률적'
Logistic Regression
- z = w0 + w1*x → g(z) (g는 시그모이드 함수)

- 확률이 1에 가까우면 output=1, 0에 가까우면 output=0
- 이 함수의 cost function을 Linear Regression과 같게 설정하면 매끈(convex)하지 않아 global minimum 찾기 어려움
cf. 대신 local minimum이 많음

- 매끈하도록 오차함수 다시 정의하면 (하나의 데이터에 대해)
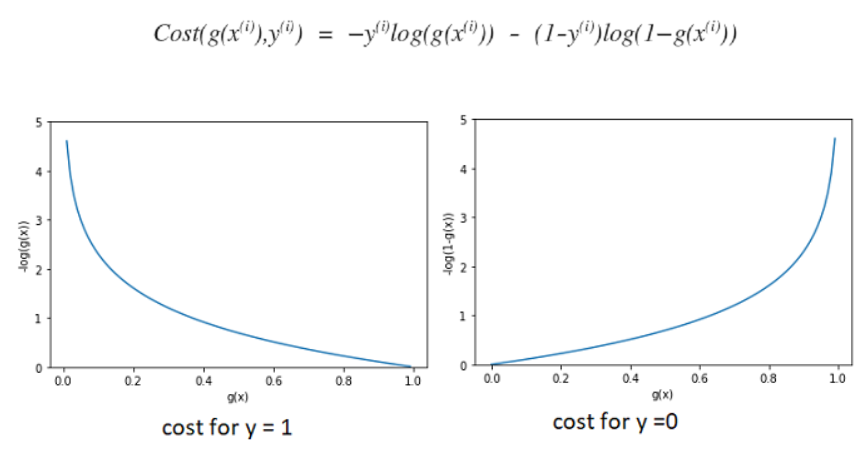
- 따라서 Logistic Regression의 오차함수는 (전체 데이터에 대해)

Under-fitting & Over-fitting
- Under-fitting : 주어진 데이터를 제대로 설명하지 못함
- Over-fitting : 주어진 데이터에만 지나치게 맞춰서 일반화 능력 부족
- 오버피팅에 대한 해결책 3가지
1) feature 개수 줄이기 (변수 줄이기)
2) 정규화 Regularization : feature는 그대로 두지만, 가중치weight를 조정해 feature의 중요도 줄이기
3) Early stopping : 일찍 학습 종료해서 일반화 능력 기르기
정규화 Regularization
1) Linear Regression with Regularization
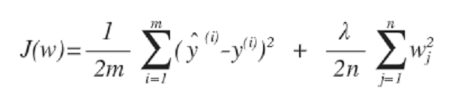
- 오차함수에 가중치 제곱의 합 더하기 (가중치 작을수록 오차 작아짐)
- lambda는 regularization parameter (하이퍼 파라미터 hyper-parameter의 한 종류)
2) Logistic Regression with Regularization
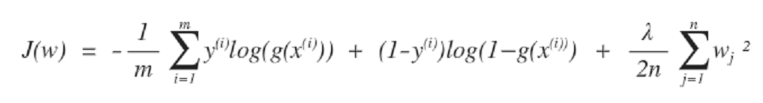
L1 정규화와 L2 정규화
1) L1 정규화(=Lasso) : 가중치 절댓값의 합을 최소화하도록 패널티(오차 증가)를 줌
- 몇몇 weight는 0으로 줄일 수 있어 feature selection 가능 (변수 몇 개쯤 아예 없앨 수 있다)
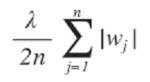
2) L2 정규화 : 가중치 제곱의 합을 최소화하도록 패널티(오차 증가)를 줌
- 모든 weight를 같은 정도로 줄이지만 아예 0으로 만들진 않음
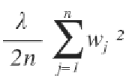
Hyper-parameters
(ex) learning rate alpha, regularization parameter lambda
Cross-Validation
- 데이터 셋의 구조
1) training data : weight, bias 등을 학습
2) validation data : hyper-parameter 학습(튜닝)
3) test data : 모델 성능 평가
- 데이터가 적어서 3개로 쪼개기 힘들면 cross-validation
- 학습 데이터를 k개로 쪼개고
2번 ~ k번으로 train, 1번으로 validation
1번, 3번~k번으로 train, 2번으로 validation
...

'nlp' 카테고리의 다른 글
| [PyTorch Tutorials] 파이토치 튜터리얼 정리/번역 (0) | 2020.02.03 |
|---|---|
| 머신러닝은 즐거워~! part 1-8 메모 (0) | 2020.02.02 |
| 밑바닥부터 시작하는 딥러닝 2권 : Chapter 7-8 [seq2seq와 어텐션] (0) | 2020.02.02 |
| 밑바닥부터 시작하는 딥러닝 2권 : Chapter 5-6 [RNN] (0) | 2020.02.02 |
| 밑바닥부터 시작하는 딥러닝 2권 : Chapter 3-4 [word2vec] (0) | 2020.01.26 |