2019. 12. 18. 15:57ㆍstats
SNUON 통계학
7-1. 이항분포
밀그램 실험
4명의 피실험자 A,B,C,D 중 정확히 1명이 볼트를 최고전압으로 올리는 걸 거부할 확률은?
A가 거부한 경우의 확률 + B가 거부한 경우의 확률 + C가 거부한 경우의 확률 + D가 거부한 경우의 확률
이항분포
- 이 경우 4가지 확률의 합이 질문의 답이다
- 이처럼 n개의 베르누이 시행에서 k개의 성공횟수를 나타내는 확률변수의 분포를 이항분포라고 한다
- 이항확률분포의 확률밀도함수는

* 이항계수 = nCk (조합)
이항분포의 평균
E(X) = np (시행횟수 * 확률)
이항분포의 분산
Var(X) = np(1-p)
예제 : 갤럽의 비만도 조사
국가주요지표 홈페이지에 의하면 2016년 한국인의 34.8%가 비만이다. 100명의 한국인을 임의로 뽑았을 때 비만인 사람은 몇 명일까?
100 * 0.348
멘델의 실험결과 조작
- 멘델의 실험결과는 too good to be true라고 알려져 있다
- 멘델의 실험에서 사용된 강낭콩의 경우 7가지 형질이 있었다. 그 중 깍지의 모양은 부푼 것(우성, i )과 수축된 것(열성, c )으로 나누어지는데 멘델이 제2세대 우성과 열성의 비율을 조사했다.
- 이 비율이 3:1에 근접하자 멘델은 우성의 모양일 경우는 i/c, c/i, i/i 의 경우라고 생각했고 이중 i/i의 비율이 1/3이 되어야 한다는 걸 보이기 위해 2세대 중 우성의 모양을 가진 강낭콩을 600개 임의로 선정했다.
- 하지만 육안으로는 우성인 모양을 가진 강낭콩이 실제로 어떤 형질을 가졌는지 알 수 없으므로 멘델은 강낭콩의 자화 수분 성질을 이용해 2세대 강낭콩에서 각각 10개의 자손을 만든 후 10개 모두 우성의 모양일 경우 2세대 모체 강낭콩을 우성으로 간주하였다.
- 이런 식으로 i/i의 개수를 세어본 결과 멘델은 총 201개의 i/i가 관측되었다고 보고했다.
- 하지만 이 경우 i/c 혹은 c/i에서도 10개의 자손이 우성의 모양으로 나올 경우가 있는데 그 확률은 (3/4)^10. 즉, 약 0.06
- 따라서 실제 우성의 모양이 관측될 기대값은 200 + 0.06 * 400 = 224이다
- 그러므로 이 모형 하에서 멘델이 201개를 관측할 확률은 약 5%다 .
Shape of Binomial Distribution
p는 고정하고 n을 늘리면 정규분포의 모양과 유사해진다
정규분포 근사에 필요한 표본크기
정규분포근사에 필요한 표본크기는 2가지 조건을 만족해야 한다
1) np >= 10
2) n(1-p) >= 10
이항분포의 정규분포 근사
- sample size가 충분히 큰 경우 이항분포는 정규분포 N(np, np(1-p))로 근사할 수 있다
예제 : 페이스북 사용자 분석
약 25%의 페이스북 사용자는 파워 사용자로 분류된다. 또한 사용자들의 평균 친구 숫자는 245명이다
245명의 친구를 가진 페이스북 사용자가 그 중 70명 이상이 파워사용자일 확률은 얼마인가?
페이스북 파워 사용자는 정규분포 근사 가능함
Bin(n=245, p=0.25) ~ N( mu = 61.25, sigma = 6.78 )

따라서 약 10%
7-2. 음이항분포
음이항분포
- 기하분포를 일반화한 확률분포
- k번째 성공을 관측할 때까지 총 시행횟수가 x일 확률은?
- 이와 같은 분포를 음이항분포라고 하고 확률밀도함수는 다음과 같이 주어진다
for x=k, k+1, ...

* x번째에 무조건 성공. 따라서 x-1번 시행까지 총 k-1번의 성공이 있어야 함
- 만약 Y = X - k , 즉 k번째 성공을 관측하기 전까지 실패횟수라고 한다면 음이항분포의 확률밀도함수는 다음과 같다
for y=0,1, ...

여기서
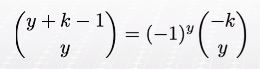
따라서 "음이항분포"라는 이름 (이항분포에 -1 붙은 것!)
"negative" binomial distribution
음이항분포의 평균과 분산
- 음이항분포의 평균 E(X) = k / p
cf. 기하분포의 평균 = 1 / p (성공이 1번)
- 음이항분포의 분산 Var(X) = k(1-p) / p^2
Shape of Negative Binmial Distributions

예제 : 정유회사의 유전탐사
정유회사가 유전을 찾기 위해 여러 군데 시추를 시행한다. 한 번의 시추마다 유전을 발견할 확률을 20%라고 하자.
1) 3번째 시추 만에 첫 번째 유전을 발견할 확률은?
0.2 * (0.8)^2 = 0.128
2) 7번째 시추만에 3번째 유전을 발견할 확률은?
6 C 2 * (0.2)^3 * (0.8)^4 = 0.049
7-3. 포아송분포
포아송분포
- 서울시민 천만 명 중 하루 평균 4.4명이 심장마비로 입원한다고 알려져 있다. 이 경우 심장마비 환자의 숫자를 나타내는 확률변수의 분포를 어떻게 표현할 수 있을까?
- 이와 같이 드문 현상의 발생 횟수를 나타내는 확률분포를 포아송분포라고 한다.
- 주로 시간, 공간이 제한된 상황에서 어떤 사건이 나타날 확률을 나타낸다
포아송분포의 확률밀도함수

포아송분포의 평균과 분산
E(X) = lambda
Var(X) = lambda
예제 : 철도사고 횟수
2017년 1억km 당 주요 철도사고의 발생건수는 평균 6회이다. 2018년의 사건횟수의 분포도 2017년과 비슷할 것이라는 가정 하에

※ 포아송분포의 평균은 정수일 필요가 없다
Shape of Poisson Distributions
평균(lambda)가 커질수록 정규분포와 유사해진다

→ 이항분포와 포아송분포 모두 (특정 조건 하에) 정규분포에 근사한다
'stats' 카테고리의 다른 글
| 9. Resampling과 가설검정 (0) | 2019.12.18 |
|---|---|
| 8. 통계적추론의 개요 (0) | 2019.12.18 |
| 6. 확률분포 (0) | 2019.11.16 |
| 5. 조건부 확률과 확률변수 (0) | 2019.11.11 |
| 4. 확률이란? (0) | 2019.10.31 |