2019. 12. 18. 16:59ㆍstats
SNUON 통계학
8-1. 표본분포
통계적 추론

- 지금까지는 평균, 특정 사건이 나타날 확률 등이 주어져있고 이를 통해 계산함
- 하지만 실제 세계에서 평균이나 확률을 정확히 알긴 어려움. 이러한 값을 추정하는 것이 통계적 추론
추정
- 우리는 데이터를 통해 모집단의 모수(population parameter)를 알아내고자 한다
- 예를 들면 모집단이 정규분포를 따른다면 모집단의 평균과 표준편차만 알면 모집단에 대한 대부분의 정보를 아는 것이다
- 일반적으로 모집단 전체를 자료로 모으는 것은 거의 불가능하므로 우리는 모집단의 일부를 sampling을 통해 표본으로 얻은 후에 표본 통계량(sample statistic)을 이용해 모집단의 모수를 추정한다.
- 데이터가 어떤 분포를 따르는지 알고, 그 분포의 parameter만 구하면 된다!
Variability in Estimates
- Sample statistic (예: 표본평균) 은 sample마다 다르다.
- 만약 우리가 sample statistic을 parameter의 추정치로 사용한다면 sample 사이의 variability를 어떠한 방식으로라도 고려해야 한다
- 먼저 이러한 sample statistic의 variability에 대해 알아보자
예제 : 서울대 통계학과 학부생들의 주량
현재 학부생은 총 146명이다. 학부생 전체를 조사하기 힘들기 때문에 10명을 골라서 조사하려고 한다
1) sample with replacement(중복 허용)로 10명의 학생을 뽑아보자
2) 10명의 학생들의 주량의 평균을 구한다
1), 2)를 여러 번 반복한 후 여기서 구해진 표본평균들의 히스토그램을 그려보자
R : sample(1:146, size=10, replace=T)
> sample : 59, 121, 88, 46, 58, 72, 82, 81, 5, 10
> 해당 번호를 가진 학생들의 주량의 평균을 구함
표본평균 : ( 8 + 6 + 10 + 4 + 5 + 3 + 5 + 6 + 6 + 6 ) / 10 = 5.9
Sampling Distribution
- 위의 과정을 얻어진 sample statistic의 분포를 sampling distribution이라고 한다
- 위에서 얻어진 표본평균의 sampling distribution은 어떤 형태를 띠고 있을까? 그리고 sampling distribution의 center를 이용해서 관심이 있는 모수인 population mean을 추정할 수 있을까?
- population mean은 5.39 (잔) 이다
Standard Error
- 추정치의 표준편차를 표준오차(standard error)라고 한다
- 표본평균의 경우 표준 오차는

예제: 두산 베어스 팬클럽 평균 경기 관전 횟수
sampling distribution with n=10, 30, 70
n을 크게 할수록 sampling distribution이 정규분포에 가까워짐
원래 모집단의 분포는 정규분포가 아니었음
모집단의 분포에 관계없이 표본평균의 sampling distribution이 정규분포에 가까워질 수 있다
중심극한정리 (Central Limit Theorem) : 표본평균의 분포는 표본크기 n이 증가하면 정규분포에 근사한다
만약 X1, X2, ... Xn이 서로 독립이고 동일한 분포를 따르면
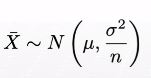
중심극한정리의 조건
1) 표본의 Independence(독립성) : sample로 뽑힌 관측치는 서로 독립이어야 한다. 다음과 같은 경우 독립을 가정한다
- random sampling이 사용된 경우
- sampling with replacement일 경우 표본크기가 모집단보다 상당히 작은 경우 (최소 10% 이하), 그러면 같은 것이 뽑힐 확률 거의 없음
* samling with replacement이면 같은 것이 뽑힐 수 있어서 절대 독립이 될 수 없음
2) Sample size : 모집단이 extremely skewed 되어 있지 않다면 n > 30 이면 일반적으로 중심극한정리를 사용할 수 있다
sample distribution이 정규분포인지 여부를 확인하는 방법?
Histogram, Normal probability plot (직선에 가까울수록 정규분포) 등
8-2. 신뢰구간 Confidence Intervals
신뢰구간
- 모집단의 모수가 가질 수 있는 값의 범위
- 신뢰구간은 point estimates의 variability를 고려한 구간 추정방법이다
- 점추정을 위해 sample statistic을 사용하는 것은 진흙탕 호수에서 창으로 물고기를 잡는거라면 신뢰구간은 그물을 사용해서 물고기를 잡는 것에 비유할 수 있다
95% 신뢰구간
- θ의 95% 신뢰구간 (L, U)는 다음과 같이 정의할 수 있다
Pr( L < θ < U ) = 0.95
* L = lower bound, U = upper bound
* L과 U는 랜덤 (sample에 따라 값이 달라짐)
- 위의 조건을 만족하는 신뢰구간은 여러 개가 있을 수 있다. 일반적으로 "좋은" 신뢰구간이란
1) 신뢰구간의 길이가 짧다
2) 신뢰구간이 이어져 있어야 한다
(ex) 대통령의 지지율이 40~42%, 50~52% 사이다 / 라고 주장하면 안 된다
- 일반적으로 추정하고자 하는 모수에 대한 95% 신뢰구간은 다음과 같이 주어진다
point estimate ± 2 * standard error ( * 2 sigma rule )
예제 : 임의로 선정한 50명의 학생에게 연애 횟수를 물어보았다. 결과는 평균 3.2회, 표준편차는 1.7회였다. 연애횟수에 대한 95% 신뢰구간을 구하여라.

95% 신뢰구간의 해석
- 학생의 평균 연애횟수가 2.7에서 3.7 사이에 있을 확률이 95%다 (X)
- 학생을 대상으로 100개의 sample을 뽑아 연애횟수에 대한 신뢰구간을 만든다면 이중 평균적으로 95개의 신뢰구간이 실제로 모집단 평균 연애횟수를 포함하고 (2.7, 3.7) 는 이렇게 구해진 100개의 신뢰구간 중 하나이다 (O)
- We're 95% confident that students on average have been in between 2.7 and 3.7 romantic relationships
- 25개의 sample을 이용하여 만든 신뢰구간에서 빨간색으로 표시된 1개의 신뢰구간은 실제 모집단의 평균연애 횟수를 포함하지 않는 경우를 보여준다
(1/25 = 4%, 약 4%의 확률로 모평균을 포함하지 않는틀린 신뢰구간이 나온다)
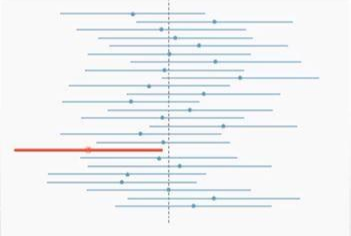
신뢰구간의 길이
신뢰수준을 95%에서 99%로 높인다면 신뢰구간의 길이는 증가한다.
95% 와 99% 신뢰구간
중심극한정리에 따라서 적절한 조건하에서 표본평균은 정규분포에 근사한다
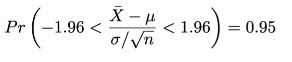
즉, mu의 95% 신뢰구간은

Margin of Error
- 표본오차 * 1.96 (2.58) 을 margin of error라고 부른다
- 표본오차에 곱하는 숫자는 정규분포의 percentile에서 나왔으며 95% 신뢰구간의 경우 97.5 percentile인 1.96 (양쪽에 2.5%가 생겨야 하므로)을 99% 신뢰구간의 경우 99.5% percentile인 2.58이 사용된다
'stats' 카테고리의 다른 글
| 10. 중심극한정리와 검정력 (0) | 2020.01.07 |
|---|---|
| 9. Resampling과 가설검정 (0) | 2019.12.18 |
| 7. 다양한 이산분포 (0) | 2019.12.18 |
| 6. 확률분포 (0) | 2019.11.16 |
| 5. 조건부 확률과 확률변수 (0) | 2019.11.11 |