2020. 1. 21. 20:58ㆍstats
SNUON 통계학
로지스틱 회귀분석
1. 단순 로지스틱 회귀분석
2. 회귀계수의 추론
3. 다중 로지스틱 회귀분석
4. Case Study
24-1. 로지스틱 회귀분석에서의 추론
회귀계수의 추정
- 로지스틱 회귀분석에서는 최대우도법을 통해서 회귀계수들을 추정한다
- 최대우도법 : 회귀계수 값을 계속 변화시키면서 주어진 자료가 관측될 확률을 가장 높게 할 회귀계수를 추정치로 선택함
- 즉 가능한 회귀계수의 값에서 주어진 자료가 관측이 될 확률을 최대로 하는 회귀계수의 값을 추정치로 사용한다
- R과 같은 통계 패키지를 사용하여 추정치와 추정치의 표준오차를 구할 수 있다
예제 : 관상동맥 심장질환
- 관상동맥 심장질환 예제에서 회귀계수의 추정치와 표준오차는 다음과 같이 주어진다

- 한 살 차이가 나는 그룹을 비교할 경우 한 살 많은 그룹이 심장질환을 가질 오즈는 어린 그룹의 오즈에 비해 1.14배 (14% 더 높다)

- 회귀계수의 신뢰구간
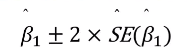
- 이 경우

- 95% 신뢰구간이 0을 포함하지 않는다. 0을 포함한다면 심장질환과 나이가 관련이 없을 수 있다는 것을 의미한다
예제 : 연령별 모유 수유 현황
- OR에 대해 95% 신뢰구간을 구하여 보자. 이 경우 베타1의 95% 신뢰구간을 이용할 수 있다

- 위 경우 신뢰구간이 1을 포함하지 않는다. 따라서 관련이 있을 수 있다.
- 1을 포함한다는 것은 OR가 1이 될 수 있다는 것을 의미하므로 반응변수(심장질환 유무)와 예측변수(나이)가 서로 관련이 없을 수 있다는 것을 의미한다
가설검정

- 여기서 null value=0 이므로

- 검정통계량의 값이 3.75이므로 정규분포를 기준으로 p-value는 0.01 이하임을 알 수 있다
- 모유수유와 연령이 관련 있다
Study design
- 로지스틱 회귀분석에서는 오즈비를 추정하기 때문에 study design에 상관없이 로지스틱 회귀분석을 사용하여 자료를 분석할 수 있다
- 만약 case-control study가 아닌 경우 상대위험도나 위험도 차이를 로지스틱 회귀분석을 사용하여 추정할 수 있을까? Yes
- 로지스틱 회귀모형이 다음과 같이 주어졌다고 하자

- 이 경우 주어진 x1 값에 대해 log(odds) 를 계산할 수 있다
- 마찬가지로 log(odds) 에서 p를 계산할 수 있다
예제 : 모유수유와 나이
모유수유 예제에서 로지스틱 회귀모형 추정치는 다음과 같다

- 24개월 된 유아가 모유수유를 하고 있을 확률은?

- 이 경우 24개월 유아가 모유수유할 오즈는 e^1.43 = 약 4.18
- 오즈비와 p의 관계

- 따라서

- 즉 24개월 유아 중 81%가 모유수유를 하고 있다고 추정된다
- 23개월 유아의 모유수유 비율을 추정해보자

- 따라서 오즈 = e^1.68 = 약 5.37
- 23개월된 유아의 모유수유 비율은
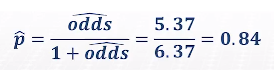
24-2. 다중 로지스틱 회귀분석
예제 : 관상동맥 심장질환
심장질환 예제에서 나이와 심장질환 사이의 관계를 다음과 같은 로지스틱 회귀모형으로 추정하였다

만약 흡연 여부(1='yes')와 심장질환 사이의 관계를 로지스틱 회귀모형으로 추정하면 다음과 같은 식을 얻을 수 있다

- 만약 두 개의 예측변수를 모두 모형에 포함시키면 어떤 결과가 나올까?
- 이 경우 다음과 같은 모형을 고려할 수 있다

- 여기서 x1은 나이, x2는 흡연 여부다
- 베타1의 추정치는 흡연여부가 같은 경우 한 살 차이가 나는 그룹 간의 log(OR)이다
- 비슷하게 베타2의 추정치는 나이가 같은 경우 흡연 여부에 따른 그룹 간의 log(OR)이다
- 흡연여부와 나이를 모두 포함하는 경우 로지스틱 회귀 모형 추정치는 다음과 같다
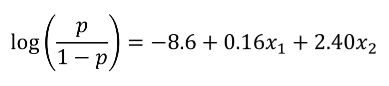
- 단순 로지스틱 회귀분석과 비교

- 나이, 흡연 모두 영향을 미치는데 흡연이 더 큰 영향을 미친다
'stats' 카테고리의 다른 글
| StatQuest Cross Validation (0) | 2021.07.07 |
|---|---|
| Micro- and Macro F1 scores (0) | 2020.10.07 |
| 23. 로지스틱 회귀분석 I (0) | 2020.01.21 |
| 22. 2x2 분할표 II (0) | 2020.01.21 |
| 21. 2x2 분할표 I (0) | 2020.01.21 |