2020. 1. 21. 19:55ㆍstats
SNUON 통계학
2x2 분할표
1. 역학설계연구
2. McNemar test for paired data
3. Fisher's exact test
4. 심슨의 역설
22-1. McNemar 검정
2x2 분할표
- 백신임상실험에 관한 지식 설문조사를 2번에 걸쳐서 실시함
- 처음 설문조사 후 6개월이 지난 후 동의서 절차를 거친 후에 두번째 설문조사를 실시
| 6개월 이후 틀림 | 6개월 이후 맞힘 | 합계 | |
| 처음에 틀림 | 251 | 178 | 429 |
| 처음에 맞힘 | 68 | 98 | 166 |
| 합계 | 319 | 276 | 595 |
- 첫번째 설문조사에서 오답율 : 429/595 = 0.72
- 두번째 설문조사에서 오답율 : 319/595 = 0.54
McNemar 검정
- Matched-Case-Control : 사례군과 대조군을 성별/나이에 따라 쌍을 이루게 하는 역학 설계연구를 말한다

- 우리는 아래 귀무가설을 검정하고자 한다 → H_0 : π_10 = π_01
- 이 경우 검정통계량(McNemar Test)은 비 대각원소의 값들이 서로 비슷한지 여부를 기반한다

- McNemar 검정통계량
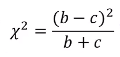
- 귀무가설 하에서 자유도가 1인 카이제곱 분포를 따른다
- 이 경우 검정통계량의 값은 48.29이며 귀무가설을 기각한다. 즉 동의서 처리 결과가 백신임상실험에 대한 이해도를 변경시켰다는 것이 통계적으로 유의하다 (이해도를 높였다, 라며 방향성을 제시할 순 없음)
22-2. Fisher의 exact 검정
피셔의 정확검정
- 표본의 크기가 작을 경우 검정통계량의 분포가 카이제곱 분포를 따르지 않을 수 있다
- 구체적으로 기대도수가 5 이하인 칸의 수가 전체 칸 수의 20% 이상인 경우 카이제곱 검정대신 피셔의 정확검정(exact test)를 사용할 것을 추천한다
차 마시는 여인
- 근대 통계학의 아버지라 불리는 피셔가 연구소 여자 동료가 홍차를 우유에 부어 마셨을 때와 우유에 홍차를 부어 마셨을 때 맛의 차이가 나며, 본인이 그 차이를 안다고 주장하자 그 주장이 맞는지 검정하기 위해 다음과 같은 실험을 행했다
- 총 8개의 컵을 준비하여 4개의 컵에는 홍차를 먼저 컵에 붓고 그 다음에 우유를 붓는다. 그리고 나머지 4개의 컵에는 역순으로 우유와 홍차를 붓고 여자 동료에게 같은 순서로 홍차와 우유를 섞은 4개의 컵을 고르게 한다
- 피셔의 실험결과는 다음과 같이 정리할 수 있다
- 귀무가설은 여자 동료가 우유와 홍차 중 어느 걸 먼저 컵에 넣었는지에 대한 감별능력이 없다
- 만약 귀무가설이 참이라면 모든 칸에서의 기대도수는 2이므로(귀무가설 하에 확률은 1/2) 카이제곱 검정을 사용할 수 없다 (칸의 100%가 5 이하)
| 추측_우유 | 추측_차 | 합계 | |
| 실제_우유 | 3 | 1 | 4 |
| 실제_차 | 1 | 3 | 4 |
| 합계 | 4 | 4 | 8 |
- 피셔는 분할표에서 만약 행과 열의 합이 고정된다면 첫 번째 열과 첫 번째 행에 해당하는 칸에서의 기대 도수는 초기하 분포를 따른다는 데에 착안하여 관측 도수가 3 이상이 될 확률을 계산한 후 이를 p값으로 사용하였다
예제 : 소금 섭취량과 심장혈관 질환 (Case-Control-Study)
- 소금섭취량과 심장혈관 질환이 관련이 있을까?
| 소금 많이 | 소금 적게 | 합계 | |
| 심장 질환O | 5 | 30 | 35 |
| 심장 질환X | 2 | 23 | 25 |
| 합계 | 7 | 53 | 60 |
- 이 경우 OR=1.90이지만 카이제곱 검정의 경우 기대값이 5 이하인 칸이 전체 칸의 25% 이상이면 그 결과를 신뢰하기 힘들다
- 이러한 경우 Fisher's exact test를 사용한다
피셔의 정확검정
- 열과 행의 합이 주어졌다고 가정한다면 이 경우 우리가 관측할 수 있는 분할표들은 다음과 같다

- 열과 행의 합이 주어졌다면, 우리가 값을 선택할 수 있는 칸은 하나뿐(나머지는 합에 의해 자동으로 정해짐). 그 값도 0-7까지만 가능
- 초기하 분포를 사용한다면 각각의 분할표를 관측할 확률을 구할 수 있다

- 즉 주어진 자료나 그보다 더 극단적인 결과를 관측할 확률(p-value)는 0.252+0.105+0.017=0.374이다
- 첫 칸이 5거나 5보다 더 큰 경우(=더 극단적인 경우)
- 따라서 귀무가설을 기각할 수 없다
22-3. 심슨의 역설
심슨의 역설 : 농구 슛 성공률
1) 3점슛 성공률
| 시도 | 성공 | 성공률 | |
| 하승진 | 50 | 20 | 40% |
| 양동근 | 54 | 22 | 41% |
2) 2점슛 성공률
| 시도 | 성공 | 성공률 | |
| 하승진 | 64 | 31 | 48% |
| 양동근 | 39 | 19 | 49% |
- 2점슛, 3점슛 성공률 모두 양동근 선수가 앞선다
- 그러나 이 둘을 합치면 전체 슛 성공률은 하승진이 앞선다
| 시도 | 성공 | 성공률 | |
| 하승진 | 50+64 | 20+31 | 45% |
| 양동근 | 54+39 | 22+19 | 44% |

- 3점슛과 2점슛을 던지는 비율이 다르기 때문에 심슨의 역설이 나타난다
- 하승진 선수가 전체에서 앞선 것은 성공률이 높은 2점슛을 더 많이 시도했기 때문이다
심슨의 역설
- 심슨의 역설은 관심이 있는 두 변주형 자료 모두에 영향을 주는 교란변수(confounder)에 기인한다
- 이 경우 교란변수의 범주별로 층화분석을 실시할 경우 두 범주형 자료의 관계를 보다 명확히 규명할 수 있다
심슨의 역설 : 미세먼지
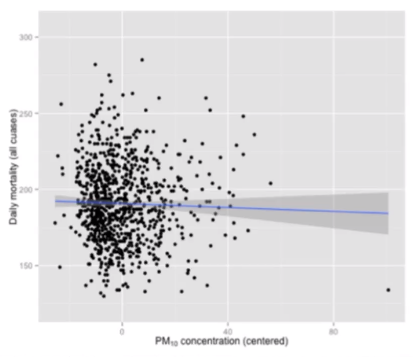

- 계절별로 나누기 전엔 미세먼지가 많을수록 사망률이 낮아짐?!
- 그러나 계절별로 나누면 미세먼지가 많을수록 사망률이 높아진다
예제 : 버클리 대학원 입시 성차별
1970년대 초반 대학원 입시에 성차별이 있었다는 이유로 버클리 대학이 고소를 당했다. 아래는 버클리 대학의 1973년 6개 대학원의 입시결과이다
| 남학생 | 여학생 | 합계 | |
| 합격 | 1198 | 557 | 1755 |
| 불합격 | 1493 | 1278 | 2771 |
| 합계 | 2691 | 1835 | 3526 |
하지만 입시결과를 학과별로 나누어서 분석한 결과 대부분의 학과에서 오히려 여학생들의 합격률이 높다는 게 밝혀졌다. 즉, 전공이 교란변수였다.
Mosaic Plot

- 합격률이 높은 학과는 남학생이, 합격률이 낮은 학과는 여학생이 많았다
'stats' 카테고리의 다른 글
| 24. 로지스틱 회귀분석 II (0) | 2020.01.21 |
|---|---|
| 23. 로지스틱 회귀분석 I (0) | 2020.01.21 |
| 21. 2x2 분할표 I (0) | 2020.01.21 |
| 20. 다중회귀분석 II (0) | 2020.01.15 |
| 19. 다중회귀분석 I (0) | 2020.01.15 |