2020. 1. 7. 16:43ㆍstats
SNUON 통계학
10-1. 중심극한정리
중심극한정리
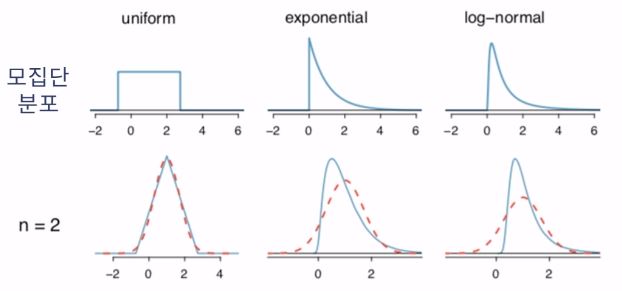
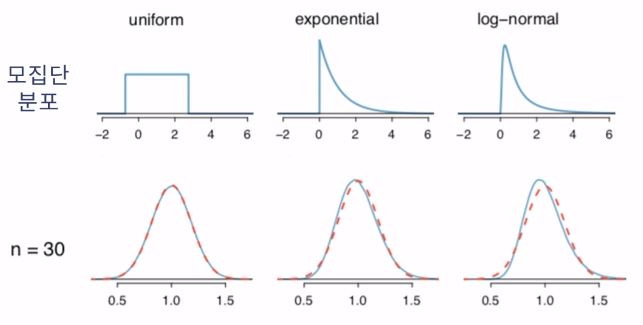
- 표본크기가 30 이상이고 모집단의 분포가 심각하게 skewed 되어 있지 않다면, 표본평균의 분포는 정규분포를 따른다
- 표본 크기가 30 이상이면 모집단의 분포와 상관없이, 표본평균의 분포는 *정규분포를 따른다
* N(모집단의 평균 , 모집단의 분산÷표본크기(n))
예제 : 모집단이 uniform, exponential, log-nrmal 분포일 때 표본평균의 분포

10-2. 표본수결정과 검정력
데이터를 보지 않고도 유의수준 5% 이하인 가설검정 만들 수 있다
(ex) 1-100까지 랜덤하게 숫자 뽑는데 1-5가 나오면 유죄, 나머지는 무죄로 판결
- 무죄인 사람 100명 오면 항상 5명은 유죄로 판결함. 따라서 유의수준은 5% 이하
- 그러나 검정력도 5%라는 문제. 유죄인 사람 100명 와도 항상 5명만 유죄로 판결함.
따라서 유의수준만 봐선 좋은 가설검정인지 알 수 없다. 검정력도 확인해야 한다
일반적으로 검정력은 80% 이상으로 설정함
주어진 margin of error를 이용한 표본 크기
- 한국 국민의 최고 혈압의 표준편차는 25mmHg이다. 서울대 학생들의 평균 최고혈압을 95% 신뢰수준에서 margin of error = 4mmHg 범위 안에서 추정을 하고자 한다. 표본크기는?
Margin of Error =
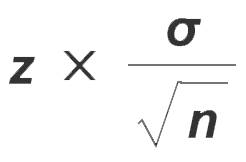
Z=1.96 (신뢰도 95%니까)
시그마 = 25 (모표준편차)
n = 구해야 할 표본크기

n >= 150.06
따라서 최소한 151명을 표본집단으로 선정해야 한다
Power와 Type 2 Error Rate
- 검정력은 귀무가설이 거짓일 때 귀무가설을 기각하는 확률
- 표본크기는 가설검정에서 검정력(power)에도 영향을 미친다
- 만약 우리가 굉장히 큰 표본을 가지고 있다면 귀무가설에서의 null value와 모집단의 parameter의 값이 아주 작은 차이만 있더라도 귀무가설을 기각할 수 있다
- 반면에 표본크기가 작을 경우 귀무가설을 기각하기 위해서 null value와 모집단의 parameter의 값의 차이가 굉장히 커야 한다
가공육류와 담배 모두 발암 1군이다. 그러나 effect size가 담배는 크고 가공육류는 작다
→ 가공육류는 엄청나게 많이 먹어야 담배 하나 폈을 때 암 발병률과 유사해진다
Effect size vs p-value
- 바나나 껍질과 자동차 모두 사고를 유발할 가능성이 크지만 두 가지는 본질적으로 다른 위험요소(risk factor)이다
- 나이가 특정 암에 미치는 영향을 조사한 결과 나이가 많을수록 암 발병률에 차이가 나지만(p-value) 1-2살 차이의 경우 발병률 차이 자체는 크지 않고 10살 정도 차이가 나야 의미있는 발병률 차이(effect size)가 나는 경우를 생각해보자
Statistically Significant vs Practically Significant
- Effect size는 "(추정치와 모수의 null value와의 차이) / 표준편차"로 정의된다
- 통계적으로 차이가 유의미한지 여부는 p-value로 정의할 수 있지만, 실질적으로 유의미한 차이가 있는지 여부는 effect size를 고려해야 한다
얼마 전 치약에 인체유해성분인 파라벤의 함유여부가 큰 논쟁거리인 적이 있었다. 이 문제를 effect size와 p-value의 개념을 사용해서 설명해보라
- 귀무가설 : 파라벤은 인체에 무해하다
- p-value 매우 작아서 인체에 유해하다 결론을 내림
- 그러나 effect size 계산해보면 매우 작음
- 하루에 양치 1000000번 닦아야 위험한 수준
'stats' 카테고리의 다른 글
| 12. 모평균에 관한 추론 II (0) | 2020.01.07 |
|---|---|
| 11. 모평균에 관한 추론 I (0) | 2020.01.07 |
| 9. Resampling과 가설검정 (0) | 2019.12.18 |
| 8. 통계적추론의 개요 (0) | 2019.12.18 |
| 7. 다양한 이산분포 (0) | 2019.12.18 |