2019. 10. 28. 13:38ㆍkhan
스탠포드 자연어 처리 강의 CS224n: Natural Language Processing with Deep Learning (http://web.stanford.edu/class/cs224n/) 를 듣고 싶었는데, 들으려면 이 4가지 조건이 우선 만족되어야 한다.


1. 파이썬
2. 미적분, 선형대수
3. 기초 확률과 통계
4. 머신러닝에 대한 기초적 이해
파이썬은 할 줄 알고, 머신러닝 개념은 대충 주워들은게 있다고 해도. 미적분, 선형대수 등 수학은 배운 적 없다!
이렇게 딥러닝에 필요한 수학을 공부할 때 많이들 추천하는 칸 아카데미! (https://ko.khanacademy.org)
머신러닝에 필요한 수학을 칸 아카데미로 공부하려는데 어떨까? 라는 질문에 달린 답변들
- 머신러닝/데이터 사이언스를 위한 수학을 공부할 땐 칸 아카데미가 최고야! So far I found Khan Academy is the best platform to learn mathematics for ML/data science
- 처음에 칸 아카데미로 선형대수, 미적분, 확률과 통계를 공부하면 엄청 도움될거야 Khan Academy is an excellent starting point, once you finish Linear Algebra, Calculus and Probability and Statistics, you will have a thorough understanding of the basics for ML.
- 머신러닝 수학을 배울 때 칸 아카데미 되게 좋아. 난 머신러닝 처음 배울 때 칸 아카데미에서 선형대수, 확률과 통계, 미적분 강의 들으면서 시작했어. Yes, Khan academy is a pretty good resource for learning ml math. I started my ml journey by refreshing my math knowledge at Khan academy by going through the following sections: Linear Algebra, Statistics and probability, Multivariable Calculus
칸 아카데미는 전 세계 7천 2백만 명의 학생들이 가입하여 학습하는 온라인 무료 교육 서비스이다. 실제 미국 학교에서 활용된다. 미국에서 만들어진 강의라 당연히 영어로 진행되는데, 네이버 비영리 교육 재단 '커넥트재단'이 칸아카데미 한국어 번역 파트너십을 맺었다. 현재 수학과 프로그래밍 분야의 강의에는 한글 자막이 제공된다.
나도 추천에 따라 칸 아카데미에서 이 3가지 강의를 듣기로 했다.
1. Linear Algebra (선형대수)
2. Statistics and Probability (확률과 통계)
3. Calculus (미분)
우선 선형대수 먼저 공부했다.
Linear Algebra > Vectors and Spaces > Vectors 부분을 정리한 것.
https://www.khanacademy.org/math/linear-algebra/vectors-and-spaces#vectors
Vectors and spaces | Linear algebra | Math | Khan Academy
If you're seeing this message, it means we're having trouble loading external resources on our website. If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
www.khanacademy.org

벡터 = 크기 + 방향 (시작점이 달라도 크기, 방향만 같으면 같은 벡터)
벡터의 덧셈
1) 산술적 덧셈 : 같은 위치에 있는 숫자끼리 더하기
2) 기하적 덧셈 : (벡터 a와 벡터 b를 더할 때) 벡터 a의 출발점에서 벡터 b의 도착점 연결하기. 이때 벡터 b는 벡터 a의 도착점에서 시작해야 함.
* a+b = b+a 이므로 a와 b의 순서를 바꿔도 무방함
벡터와 스칼라의 곱셈
(ex1) 3 * 벡터 a : 방향은 같고, 벡터 a의 크기만 3배가 됨
(ex2) (-3) * 벡터 a : 방향은 반대, 벡터 a의 크기는 3배가 됨
* 스칼라가 음수인 경우 벡터의 방향이 반대가 됨
벡터의 뺄셈
1) 산술적 뺄셈 : 같은 위치에 있는 숫자끼리 뺄셈
2) 기하적 뺄셈 : 두 벡터가 같은 곳에서 시작할 경우, 두 벡터의 양 끝점(도착점)을 연결하기
단위 벡터 = 길이가 1인 벡터
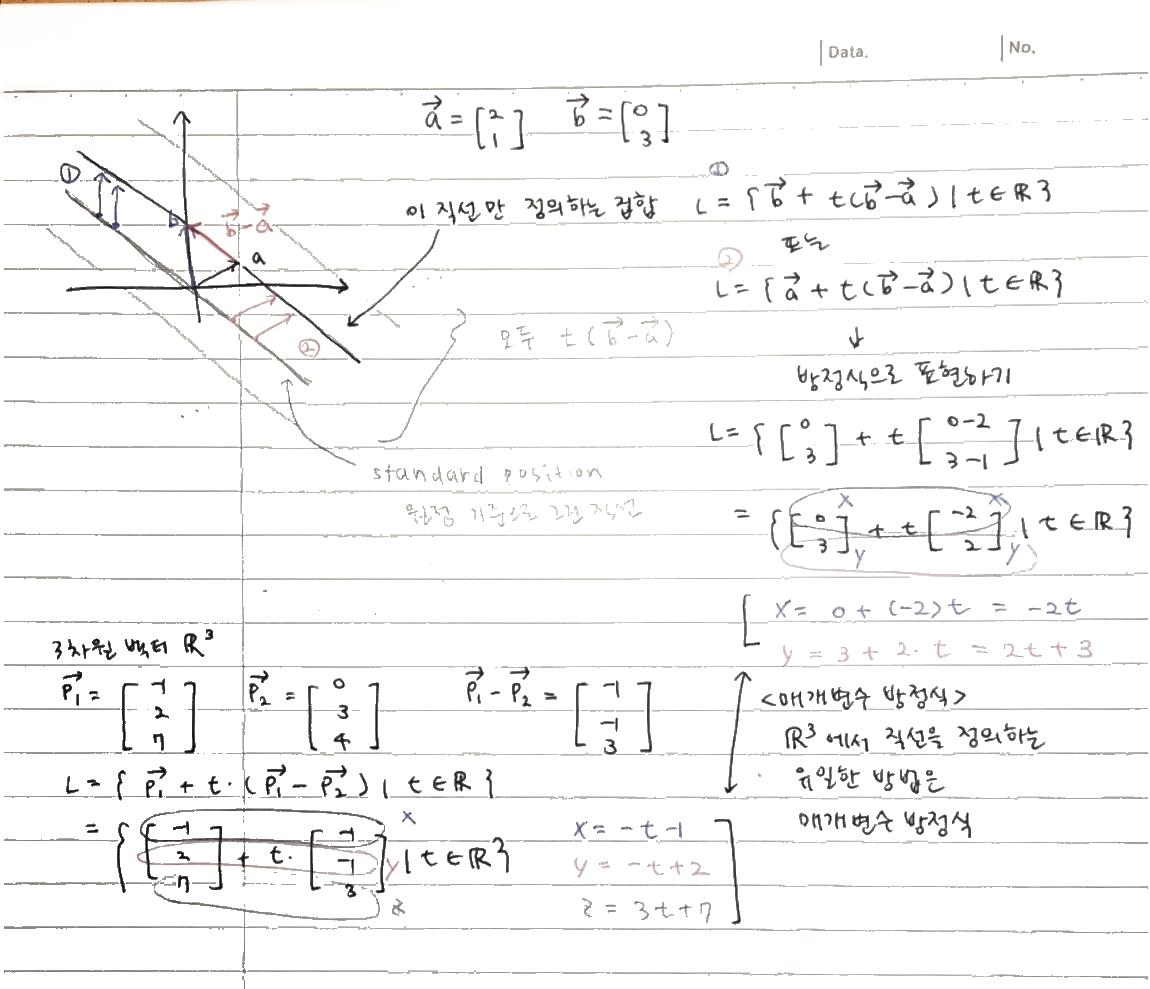
매개변수 방정식
• 벡터를 이용해 직선을 매개변수로 나타내기
• L = { x + t * v | t는 실수} * x와 v는 벡터, t는 상수
→ 2차원뿐만 아니라 n차원에서 모두 적용 가능하다


이번 강의에서 배운 단위벡터, 다음 강의에서 배울 선형결합의 개념이 PCA에 사용된다.
머신러닝/통계 분야의 어려운 개념을 완전 쉽게 설명해주는 유튜브 StatQuest
https://www.youtube.com/watch?v=FgakZw6K1QQ

'khan' 카테고리의 다른 글
| 칸 아카데미로 딥러닝을 위한 수학 공부하기 | Vector dot and cross products (2) (0) | 2019.11.18 |
|---|---|
| 칸 아카데미로 딥러닝을 위한 수학 공부하기 | Vector dot and cross products (1) (0) | 2019.11.15 |
| 칸 아카데미로 딥러닝을 위한 수학 공부하기 | Subspaces and the basis for a subspace (0) | 2019.11.08 |
| 칸 아카데미로 딥러닝을 위한 수학 공부하기 | Linear dependence and independence (0) | 2019.11.04 |
| 칸 아카데미로 딥러닝을 위한 수학 공부하기 | Linear Combinations and Spans (0) | 2019.10.30 |