2019. 12. 4. 14:04ㆍnlp
Edit Distance : 한 스트링이 다른 스트링으로 되기까지 필요한 editing operation의 최소 횟수
editing operation : insertion(1), deletion(1), substitution(2) (괄호 안은 각 operation의 cost, Levenshtein)
* Levenshtein은 substitution의 cost를 2로 본다 ∵ insertion(1) + deletion(1) = substitution(2)
모든 distance 계산하기 어려움. 그래서 Dynamic Programming 도입
Dynamic Programming
- 복잡한 계산 = subproblems를 합쳐서 구해가기
- bottom-up 방식
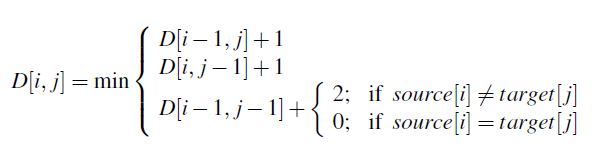
예를 들어, INTENTION을 EXECUTION으로 바꾸는 거리를 계산한다고 하자. D[2,3]은 source의 첫 두글자인 'IN'을 target의 첫 세글자인 'EXE'로 바꾸는데 필요한 cost이다. 이를 D[1,3], D[2,2], D[1,2]를 활용하여 계산할 수 있다.
우선 D[1,3]은 'I'를 'EXE'로 바꾸는데 필요한 cost이다. 'I'를 'E'로 substitute하고 X와 E를 삽입하면 되므로 총 cost는 2+1+1=4이다. 이를 통해 D[2,3]을 계산할 수 있다. 'IN'을 'EXE'로 바꾸려면 'I'를 'EXE'로 바꾸는데 필요한 4 + N을 삭제하는데 필요한 1만 더해주면 된다. 따라서 5가 된다.

cost를 최소화해주도록 두 스트링을 align해주려면 backtrace가 필요하다. 위의 표를 이용해 minimum edit distance를 구하고, 그 edit distance가 어디서 왔는지 알려주는 표시다.
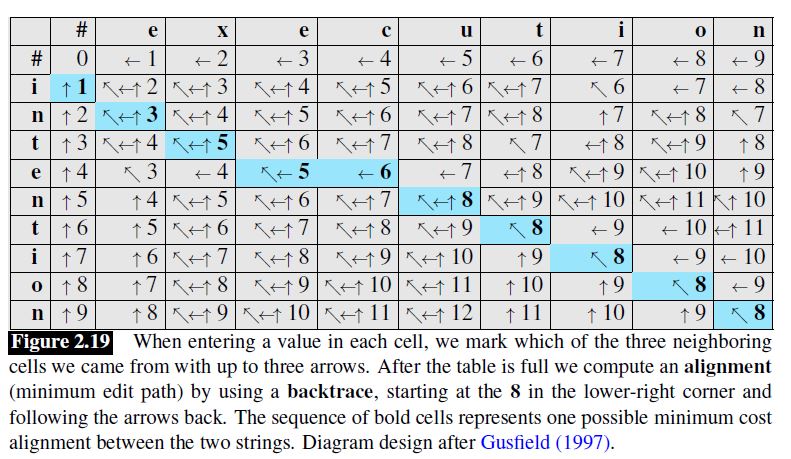
한 칸을 채우려면 주변 칸의 숫자를 이용해서 채울 수 있다. 위 또는 왼쪽 칸의 +1 값(삭제 또는 삽입), 대각선 칸의 +2(해당 칸의 source 문자와 target 문자가 같은 경우 +0) 중 최솟값을 택하면 된다. 그래서 그 숫자가 어느 칸에서 왔는지 화살표로 표시한다. 세 경우의 값이 모두 같으면 세가지 화살표 모두 표시한다.
Weighted Edit Distance
삽입, 삭제, 대체에 따른 cost를 다르게 할 수도 있다. 예를 들어 타이핑할 때 a와 s는 키보드 바로 옆자리이다. 따라서 a를 멀리 있는 l로 잘못 치는 경우보다 a를 바로 옆의 s로 잘못 치는 경우가 많을 것이다. 이런 상황을 모두 계산하여 서로 다른 cost를 줄 수도 있다.
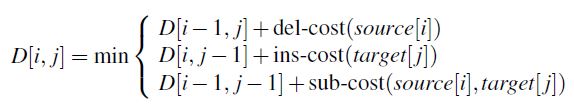
여기서 직접 Levenshtein 방식으로 Edit Distance를 계산해볼 수 있다.
Levenshtein Demo
www.let.rug.nl
※ 출처
1) 글 버전
2) PPT 버전
'nlp' 카테고리의 다른 글
| Naive Bayes and Text Classification (0) | 2019.12.04 |
|---|---|
| Language Modeling (0) | 2019.12.04 |
| 정규표현식 정리 (0) | 2019.12.04 |
| 넷플릭스/네이버 시놉시스 어휘 단계 분석하기 (0) | 2019.11.11 |
| 넷플릭스/네이버 시놉시스 품사 분석하기 (3) | 2019.11.04 |