2019. 12. 4. 16:44ㆍnlp
목차
1. 정보량 수량화하기
2. Entropy (엔트로피)
3. Cross Entropy (교차 엔트로피)
4. Cross Entropy와 Perplexity(혼잡도)
1. 정보량 수량화하기
1) 중요성 : 일어날 확률 낮을수록 정보량이 많다

2) 가법성 : 두 사건이 독립이라면 두 사건이 함께 일어날 때의 정보량은 각 사건의 정보량을 합한 것과 같다

이 두가지 조건을 만족시키려면 정보량은 다음과 같이 정의되어야 한다. 이는 놀라움의 정도로 해석할 수 있다.

2. Entropy (엔트로피)
엔트로피는 표본공간에 나타나는 모든 사건의 정보량의 평균적인 기댓값

이러한 엔트로피는 확률이 모두 같을 때 (uniform distribution) 가장 높다.
(ex) fair coin이라 앞면 뒷면 나올 확률 같을 때 가장 예측하기 어렵다. 따라서 엔트로피가 높다. 그러나 biased coin이라 앞면이 나올 확률이 더 높다고 하자. 그러면 앞면이 나와도 크게 놀랍지 않다(예측하기 쉽다). 따라서 엔트로피가 낮다.
특정 단어 연쇄의 엔트로피는
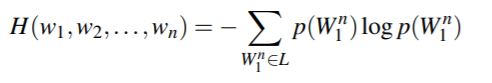
이를 단어의 개수 n으로 나누면 per-word entropy, 즉 entropy rate가 된다.

이 단어의 연쇄가 무한히 길면 한 언어의 엔트로피를 구할 수 있다.

이 복잡한 수식은 Shannon-McMillan-Breiman Theorem으로 단순화할 수 있다. 언어는 어느 정도 규칙적이므로 충분히 긴 연쇄를 사용하면 그 안에 다양한 연쇄가 포함되어 있다. 따라서 다양한 연쇄를 다 더하지 않아도 된다는 이론이다.

3. Cross Entropy (교차 엔트로피)
그러나 사실상 긴 단어 연쇄의 실제 확률을 구하긴 어렵다. 그래서 이 확률을 추정한 모델을 만들고, 이 모델이 추정한 확률에 근거해 entropy를 계산해야 한다. 이러한 entropy가 cross entropy이다.

이 수식도 Shannon-McMillan-Breiman Theorem으로 단순화할 수 있다.

이렇게 구한 cross entropy는 실제 entropy보다 항상 크거나 같다. 따라서 다양한 모델로 cross entropy를 구하고, 이 중 가장 낮은 걸 취하면 점점 실제 entropy에 가까워질 수 있다.

4. Cross Entropy와 Perplexity(혼잡도)
cross entropy는 text processing에, perplexity는 음성 인식 분야에 많이 사용된다.


※ 출처 : 이 글의 20페이지부터
'nlp' 카테고리의 다른 글
| 밑바닥부터 시작하는 딥러닝 1권 : Chapter 2-4 [퍼셉트론과 신경망] (0) | 2019.12.24 |
|---|---|
| Maximum Entropy Model (0) | 2019.12.04 |
| Vector Semantics (0) | 2019.12.04 |
| Naive Bayes and Text Classification (0) | 2019.12.04 |
| Language Modeling (0) | 2019.12.04 |