2020. 1. 21. 18:24ㆍstats
SNUON 통계학
2x2 분할표
1. 역학설계연구
2. McNemar test for paired data
3. Fisher's exact test
4. 심슨의 역설
21-1. 역학연구설계 Study Design
자료 유형별 분석방법
| 반응변수_이산형 | 반응변수_연속형 | |
| 설명변수_이산형 | 분할표 분석 | 분산분석 |
| 설명변수_연속형 | 로지스틱 회귀분석 | 회귀분석 |
예제1 : 아스피린과 심근경색
40세에서 84세 사이의 남자의사 22,071명을 대상으로 절반은 아스피린, 나머지 절반은 위약(placebo)을 준 후 심근경색 발병 여부를 조사
| 심근경색 O | 심근경색 X | 합계 | |
| 아스피린 | 104 | 10,933 | 11,037 |
| 위약 | 189 | 10,845 | 11,034 |
| 합계 | 293 | 21,778 | 22,071 |
질문 : 아스피린이 심근경색 예방에 도움을 주는가?
예제2 : 구강암과 흡연과의 관계
| 흡연 | 비흡연 | 합계 | |
| 구강암 | 484 | 27 | 511 |
| 구강암 X | 385 | 90 | 475 |
| 합계 | 869 | 117 | 986 |
질문 : 흡연이 구강암과 관련이 있는가? 그렇다면 흡연자가 구강암에 걸릴 가능성을 비흡연자와 비교한다면 얼마나 높은가?
예제3: 임금과 직업 만족도
1984년 미국 성인을 대상으로 한 임금과 직업 만족도에 대한 설문조사
| 불만족 | 만족 | 합계 | |
| $15,000 이하 | 4104 | 391 | 495 |
| $15,000 이상 | 66 | 340 | 406 |
| 합계 | 170 | 731 | 901 |
질문 : 연봉과 직업만족도는 관련이 있는가? 그렇다면 그 영향력은 어느 정도인가?
예제4 : 백신임상실험에 대한 인식 조사
백신임상실험에 관한 지식 설문조사를 2번에 걸쳐 실시함
처음 설문조사 후 6개월이 지난 후 동의서 절차를 거친 후에 두 번째 설문조사를 실시한다
| 6개월 이후 틀림 | 6개월 이후 맞힘 | 합계 | |
| 처음에 틀림 | 251 | 178 | 429 |
| 처음에 맞힘 | 68 | 98 | 166 |
| 합계 | 319 | 276 | 595 |
질문 : 동의서 처리절차가 백신임상실험에 관한 이해도를 높이는데 기여하였는가?
역학연구 설계 : 코호트(cohort) 연구 (예제1)
- 특정 위험요인에 노출된 집단과 노출되지 않은 집단의 질병발생률을 비교 분석하여 위험요인과 질병 사이의 관련성을 조사
- p1 = 위험에 노출된 집단의 질병발생률
- p2 = 위험에 노출되지 않은 집단의 질병발생률
- 상대위험도(Relative Risk) : RR = p1 / p2
- 위험도 차이(Risk Difference) : RD = p1 - p2
- 오즈비(Odds Ratio) : OR = { p1 / ( 1 - p1 ) } / { p2 / ( 1 - p2 ) }
역학연구 설계 : 사례-대조군(case-control) 연구 (예제2)
- 환자와 대조군 각각에서 과거에 위험요인에 노출된 정도를 비교하여 질병과 위험요인과의 관련성을 알고자 한다
- 여기서 계산된 오즈비는 코호트 연구에서 계산되는 오즈비와 수학적으로 동일하다
- 상대위험도를 계산할 수 없으므로 오즈비만 유일한 관련성 측도이다
- 희귀한 질병에 대해서 오즈비와 상대위험도는 비슷하다
- p1 = 흡연자 중에 구강암에 걸린 비율
- p2 = 비흡연자 중에 구강암에 걸린 비율
- 주어진 자료만으로는 상대위험도를 구할 수 없음 (흡연자, 비흡연자로 구한게 아니라 구강암 발병 여부에 따라 자료를 구해서)
- 사회과학 연구는 대부분 사례-대조군 연구 (10살 짜리 아이 50명, 50명씩 뽑아서 한 집단에 강제로 담배를 피우게 할 수 없으므로)
역학연구 설계 : 단면조사(cross-section) 연구
- 질병의 유병상태와 위험요인의 노출간의 관련성을 특정 시점 또는 기간 동안에 조사하는 것
- 상대위험도, 위험도 차이, 오즈비 모두 계산할 수 있다
2x2 분할표에서 OR, RR의 추정
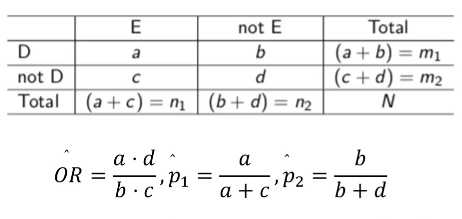
- RR=1, RD=0, OR=1 이면 위험요인과 질병이 관련이 없다는 의미
- 일반적으로 위험요인이 맞다면 RR, OR은 1보다 큰 값
예제 : 코호트 연구
- 임상실험을 통한 아스피린과 심장마비와의 관련성에 대한 연구
- 40세에서 84세 사이의 남자 의사 22,071명을 대상으로 절반은 아스피린, 나머지 절반은 위약(placebo)를 준 후 심슨경색 발병 여부를 조사함
- 심근경색 발병율은 아스피린 그룹 중에는 0.94%(=104/11,037)인 반면 위약 그룹에서는 1.71%(=189/11,034)이었다
| 심근경색 O | 심근경색 X | 합계 | |
| 아스피린 | 104 | 10,933 | 11,037 |
| 위약 | 189 | 10,845 | 11,034 |
| 합계 | 293 | 21,778 | 22,071 |
- 이 예제의 경우 임상실험결과가 2x2 분할표로 정리되어 있고 우리가 관심있는 것은 각 그룹별 위험도(원치 않는 결과가 나온 경우, 이 예제에서는 심근경색)의 차이를 알아보는 것이다
- 위험도 = (심근경색 환자의 수) / (각 그룹에 참여한 의사들의 수)
- 2x2 분할표에서 두 범주형 변수의 관련성에 관한 측도 : 상대위험도, 오즈비
상대위험도(Relative Risk)
- 상대위험도(RR)의 경우 두 위험도의 비로 나타낼 수 있다
- 상대위험도 = (첫번째 범주에서 위험도) / (두번째 범주에서 위험도)
- 이 예제에서 심근경색의 상대위험도는 0.94/1.71 = 0.55로서 아스피린 복용시 심근경색을 일으킬 확률이 위약복용그룹 확률의 0.55배이다
- 아스피린 복용은 위험요인이 아니라 도움 요인이므로 보다 자연스러운 해석은 아스피린 복용시 심근경색 발병률이 (1-0.55)*100 = 45% 낮추어졌다고 얘기할 수 있다
오즈비(Odds Ratio)
- 위험의 오즈 = 위험도 / (1-위험도)로 정의된다. 예를 들면 오즈가 4라는 것은 위험이 발생할 확률이 그렇지 않을 확률의 4배라는 것이다. 이 예제의 경우 아스피린 그룹에서 심근경색의 오즈는 0.0094/(1-0.0094) = 0.0095로서 위험도와 비슷하다
- 오즈비(OR)는 두 오즈의 비율을 나타낸다. 상대위험도는 확률의 비율인데 위험도가 아주 낮을 경우 오즈비와 상대위험도는 유사한 값을 나타낸다
- 오즈비는 위험요인과 질병을 서로 바꾸어도 같은 값을 가진다
- (아스피린 그룹에서 심근경색의 오즈) / (위약 그룹에서 심근경색의 오즈) = (104/10933) / (189/10845) = 0.546
- (심근경색 발병 그룹에서 아스피린 복용의 오즈) / (정상그룹에서 아스피린 복용의 오즈) = (104/189) / (10933/21778) = 0.546
예제 : 사례 대조군 연구
- 우리는 흡연이 구강암의 원인인지 알고 싶다
- 구강암 환자들 중 흡연여부에 대한 조사를 하고 비슷한 성격(성별, 연령 등)의 대조군에 대해서도 흡연 여부를 조사하여 결과를 정리했다
- 사례군(구강암 환자)과 대조군의 참여 인원을 비슷하게 맞춘 결과 흡연자들이 월등히 많이 참여했음을 알 수 있다. 이 경우 상대위험도를 계산하는 것은 의미가 없다
| 흡연 | 비흡연 | 합계 | |
| 구강암 | 484 | 27 | 511 |
| 구강암 X | 385 | 90 | 475 |
| 합계 | 869 | 117 | 986 |
- 하지만 이 경우 구강암의 오즈비는 계산이 가능하다. 즉, (흡연자 그룹에서 구강암의 오즈) / (비흡연자 그룹에서 구강암의 오즈) = (구강암 그룹에서 흡연의 오즈) / (대조군에서 흡연의 오즈)가 같다는 사실을 이용하여 구강암의 오즈비를 구할 수 있다
- 이 경우 OR = 484*90 / 27*385 = 4.19이며 이에 대한 해석은 흡연자 그룹에서 구강암의 오즈 추정값은 비흡연자 그룹에서 구강암 오즈의 4.19배이다
(코호트 연구처럼 해석 가능)
2x2 분할표 분석 정리
- 2x2 분할표에서 두 범주형 변수 연관성의 측도로는 상대위험도와 오즈비가 있다
- 사례 대조 연구에서 상대 위험도를 계산하는 것이 불가능하므로 오즈비를 계산하고 희귀 질병의 경우 오즈비와 상대위험도가 비슷하다는 것을 이용하여 상대 위험도에 대한 근사값으로 사용한다
- 독립성 검정은 오즈비 또는 상대위험도가 1인지 여부를 검정하는 것과 동일하다
사례연구 : 단면조사 연구
- 임금이 낮은 그룹에서 직업에 불만인 비율은 391/495=0.2이고 높은 그룹에서 불만족자의 비율은 340/495=0.16이며 상대위험도는 1.29 (95% 신뢰구간 0.98-1.71)이지만 신뢰구간이 1을 포함하고 있기 때문에 두 비율이 다르다고 할 수 없다
| 불만족 | 만족 | 합계 | |
| $15,000 이하 | 4104 | 391 | 495 |
| $15,000 이상 | 66 | 340 | 406 |
| 합계 | 170 | 731 | 901 |
'stats' 카테고리의 다른 글
| 23. 로지스틱 회귀분석 I (0) | 2020.01.21 |
|---|---|
| 22. 2x2 분할표 II (0) | 2020.01.21 |
| 20. 다중회귀분석 II (0) | 2020.01.15 |
| 19. 다중회귀분석 I (0) | 2020.01.15 |
| 18. 회귀분석 III (0) | 2020.01.15 |