2020. 1. 15. 21:13ㆍstats
SNUON 통계학
다중회귀 Multiple Regression
1. 다중회귀분석
2. 모형선택
3. 그래프를 이용한 회귀분석의 가정점검
4. 로지스틱 회귀분석
19-1. 다중회귀분석의 소개
Multiple Regression
- 단순회귀분석 : 설명변수가 1개인 경우
- 다중회귀분석 : 설명변수가 여러 개인 경우
어린왕자 예제

Hardcover vs Paperback
- 단순회귀분석 : volume과 weight 사이의 관계를 hardcover와 paperback 별로 나누어 살펴보자

Modeling weights of books using volume and cover type

- 나머지 변수의 값이 모두 같다는 전제하에 (커버가 같은 종류라면) volume이 1 단위 증가하면 weight는 0.71795 증가한다
- volume이 같고 paperback이라면 weight는 184.0473만큼 감소한다
- Slope of volume : 책의 커버 종류가 같은 경우 책의 무게는 1세제곱 센티미터마다 0.72 그램 더 나간다
- Slope of cover : volume이 같을 경우 paperback의 무게가 hardcover bok의 무게보다 평균적으로 184 그램 가볍다
Reference Level
- 커버의 reference level = hardcover
- papberback이면 1, hardcover면 0
→ weight_hat = 197.96 + 0.72*volume - 184.05 * cover:pb
1) Hardcover books : weight_hat = 197.96 + 0.72*volume
2) Paperback books : weight_hat = 197.96 + 0.72*volume - 184.05 * 1 (절편의 값이 작아진다)

아이의 키, 몸무게, 팔목 두께
- 단순회귀분석 : 키-몸무게, 키-팔목 두께, 몸무게-팔목 두께 모두 양의 상관계수를 가짐
- 그러나 다중회귀분석의 경우 상관계수의 부호까지 달라질 수 있음
- 회귀는 나머지 변수를 통제한 후 두 변수의 관계를 측정하는 것!
- 같은 몸무게인 두 아이라면, 키가 커질수록 팔목이 가늘어짐 (음의 상관)
Interpretation of the regression coefficient

Another example : Modeling kid's scores
어머니의 특징을 사용하여 3-4살 어린이의 인지능력점수를 예측하고자 한다

기울기의 해석

- mom_hs/work 의 reference level = no 졸업하지 못한 경우 ( mom_hs/work:yes = 1 / no = 0 )
- 엄마의 학력, IQ는 p-value < 0.05. 따라서 기울기가 0 아님
- 다른 모든 조건 (엄마의 나이, 학력, 직업)이 같다면 엄마 IQ가 1 높은 경우 자녀의 IQ는 평균적으로 0.56 높다
- 절편의 해석? 고등학교를 졸업하지 않고 아이가 태어난 후 첫 3년간 일하지 않았으며 IQ가 0? 인 엄마의 자녀들의 평균 IQ는 19.59 (의미 X)
Revisit : Modeling poverty
50개주의 빈곤율

여성 세대주 비율을 이용한 빈곤율 예측 (단순회귀분석)

- 여성 세대주 비율이 1% 증가하면 빈곤율은 0.68% 증가한다
- R^2 = 0.28 : 이 모형이 반응변수(빈곤율) 변동(=분산)의 28%를 설명한다 (그리 높은 설명력 아님)
R^2의 3가지 계산 방법
1) x와 y의 상관계수의 제곱
2) y_hat과 y의 상관계수의 제곱
3) 원래 정의

Sum of Squares

3가지 방법을 사용하는 이유?
- 단순회귀분석에서는 3가지 방법 모두 사용할 수 있다
- 다중회귀분석에서는 (첫 번째 방법 빼고) 2가지 방법을 사용할 수 있다
- R^2 특징 중의 하나는 변수를 추가할수록 증가한다는 것이다. 그렇다면 R^2이 높으면 좋은 모형일까?
빈곤율 예측에 두 예측변수를 사용할 경우

백인의 비율을 추가하는 것이 빈곤율 예측에 도움을 주는가?
- female_house와 white의 상관계수는 -0.75. 큰 관련이 있음. 그래서 빈곤율 예측에 비슷비슷한 두 변수를 넣은 셈! 따라서 R^2 수치가 크게 늘지 않음
- 기존의 변수인 female_house랑 상관이 크게 없으면서 poverty와는 상관있는 새로운 변수를 추가해야 R^2(설명력)가 증가함
Colinearity between predictors
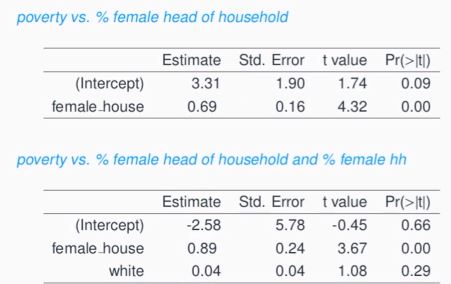
- female_house와 white의 상관계수가 커서 뒤죽박죽
- 두 변수가 크게 관련 없었다면 기존 female_house의 slope이 크게 변화하지 않았을 것! (지금은 0.69 에서 0.89 로 크게 증가)
- female_house와 white가 correlated
Colinearity between predictors
- 예측변수들이 서로 관련이 있을 때 colinearity가 존재한다고 한다
- 관련이 있는 예측변수를 모형에 추가할 경우 실제 예측에 도움을 거의 주지 않는다
- 관측연구에서는 colinearity가 거의 항상 존재하고 실험에서는 예측변수들 사이가 독립이 되도록 설계하는 것이 중요하다
R^2 vs. adjusted R^2

- 예측변수를 추가하면 R^2는 항상 증가한다
- 좋은 모형을 결정하는 기준으로 R^2 대신 adjusted R^2을 사용할 수 있다

cf. R^2 = 1 - (SS_error) / (SS_total)
- 여기서 p는 예측변수의 개수를 의미하며 n은 자료의 개수이다
- p가 많아질수록 (n-1)/(n-p-1) 은 1보다 커진다. R^2에 비해 1에서 더 큰 값을 빼게 되므로 adjusted R^2 은 더 작아진다
- adjusted R^2 은 예측변수가 많아지는 경우 R^2에 패널티를 준 것이라고 생각할 수 있다
- 따라서 adjusted R^2를 모형선택의 기준으로 사용할 수 있다
Adjusted R^2 계산하기

dsd
sd
'stats' 카테고리의 다른 글
| 21. 2x2 분할표 I (0) | 2020.01.21 |
|---|---|
| 20. 다중회귀분석 II (0) | 2020.01.15 |
| 18. 회귀분석 III (0) | 2020.01.15 |
| 17. 회귀분석 II (0) | 2020.01.15 |
| 16. 회귀분석 I (0) | 2020.01.15 |