2020. 1. 15. 22:21ㆍstats
SNUON 통계학
20-1. 모형선택 Model Selection
강의평가와 외모
- University of Texas 학생들을 대상으로 강사의 외모와 강의평가를 실시하게 하였다
- 6명의 학생들로 이루어진 별도의 평가단이 강사의 외모를 평가하였으며 이 학생들은 해당수업 수강생은 아니었다
외모와 강의평가 단순회귀분석

- p-value < 0.05 니까 통계적으로 유의미한가? 그런데 기울기 값이 0.13밖에 안 됨
- 데이터가 매우 많음. 검정력(Power)도 커져서 귀무가설 쉽게 기각
- 예를 들어 실제 기울기 값은 0.0001 인데 0은 아니니까 귀무가설 기각 가능
- R^2 을 보아 3% 정도 설명 가능한 모델
성별에 따른 차이가 있는가?
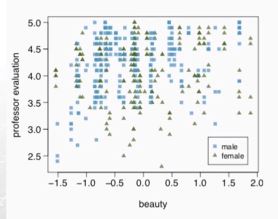

→ 외모가 같다는 가정 하에 남성 교수가 여성 교수보다 강의점수가 0.17점 만큼 높다
강의평가와 외모 (Full model)

→ 총 변수 10개. 따라서 만들 수 있는 모델은 총 2^10 = 1024 개 (1개,2개,...,10개 변수 포함한 모델 등)
Q. 위의 표에서 p-value >= 0.05 인 변수만 빼면 최적의 모형?
A. No. 변수 하나 뺄 때마다 p-value 달라짐. Colinearity가 존재하기 때문.
모형 선택 방법
1) Backward-elimination
2) Forward-selection
1) Backward-elimination
full model에서 시작해 하나의 변수를 drop
그러면 9개의 변수가 있는 10개의 모델이 생김
이 10개 모델의 성능을 adjusted R^2 또는 p-value로 평가
- adjusted R^2 가 증가하지 않을 때까지 반복하며 변수 drop
- 모든 p-value < 0.05 일 때까지 반복하며 변수 drop

1) -1 Adjusted R^2

...
반복하다가 R^2 더이상 증가하지 않으면 멈춤
1)-2 P-value

2) Forward-selection
반응변수만 있는 상태에서 변수 하나씩 추가
그러면 반응변수1, 설명변수1 인 10개의 모델이 생김
- adjusted R^2 가 최대인 모델 선택하고 adjusted R^2 가 증가하지 않을 때까지 반복하며 변수 추가
- p-value가 최소인 모델 선택하고 p-value > 0.05 되면 변수 추가 그만하기

20-2. 그래프를 이용한 회귀분석모형 가정에 관한 점검
Model Conditions
1) 잔차가 거의 정규분포
2) 잔차가 등분산성 ( x값에 상관없이 분산이 일정함)
3) 잔차가 서로 독립
4) 각 독립 변수가 결과에 대해 선형적으로 관련이 있다

1) Model residuals
정규성 검증 (크게 skewed 되지만 않으면 OK)

2) Constant variance
x 값의 증가/감소에 따라 특정한 패턴을 보이지 않으면 등분산성
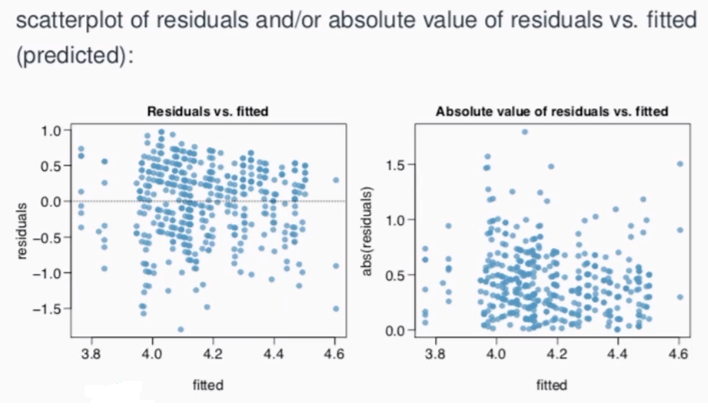
- 단순회귀분석에서는 y축에 잔차, x축에 x 설명변수(단순회귀 분석이라 변수 1개) 그려서 등분산성 확인함
- 다중회귀분석에서는 y축에 잔차, x축에 y의 추정치 (= 여러 x들의 선형결합) 그려서 등분산성 확인함
3) Independent residuals
패턴이 보이면 독립이 아닌 것 (ex. 시계열 데이터는 패턴이 보임. 독립 아님)

4) Linear relationships
모든 설명변수와 반응변수가 선형관계여야 함

'stats' 카테고리의 다른 글
| 22. 2x2 분할표 II (0) | 2020.01.21 |
|---|---|
| 21. 2x2 분할표 I (0) | 2020.01.21 |
| 19. 다중회귀분석 I (0) | 2020.01.15 |
| 18. 회귀분석 III (0) | 2020.01.15 |
| 17. 회귀분석 II (0) | 2020.01.15 |