2020. 1. 7. 18:39ㆍstats
SNUON 통계학
Inference for Numerical Data
1. 일 표본평균과 t-분포
2. Paired data에 관한 추론
3. 두 표본평균의 차이에 관한 추론
4. Power Analysis
5. ANOVA
11-1. 단일표본 평균과 t-분포
통계적 추정의 과정
1) 가설검정
2) 점 추정치, 구간 추정치(신뢰구간)
13일의 금요일은 정말 불길한 날짜인가?
- 이 연구의 목적은 사람들의 행동방식이 13일의 금요일과 그 전주인 6일의 금요일이 차이가 있는지 알고자 하는데 있다
- 이 두 날짜의 교통량을 비교하는 것으로 사람들의 행동양식을 비교하고자 했다
- 질문 : 연구자들은 왜 이러한 비교방식을 선택했을까?
1) 가설검정
- H0 : 13일 금요일과 6일 금요일의 평균 교통량은 같다
- HA : 13일 금요일과 6일 금요일의 평균 교통량은 다르다
각각의 경우 교통량은 같은 해 같은 달 같은 장소에서 일주일 간격으로 측정하였다
이 경우 교통량들은 서로 독립인가?
- 일주일 간격의 교통량은 서로 독립이 아니므로 교통량의 차이가 0인지 여부를 확인하고자 한다
- 이 경우 교통량의 차이들간은 서로 독립이라고 할 수 있다
교통량 차이의 히스토그램은 다음과 같다. Skewed 분포라고 보기는 어렵지만, 표본 숫자가 너무 작기 때문에 중심극한정리를 적용하긴 힘들다
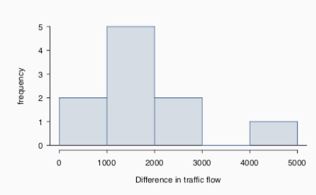
표본평균이 정규분포를 따르지 않는 경우도 있다 ∵ 표본 크기가 작아서
t-distribution
- 모집단의 표준편차가 알려져 있지 않은 경우 표본 표준편차로 모집단의 표준편차를 추정한다. 이때 추가로 생기는 불확실성을 포함하기 위해 새로운 분포가 필요하다
- 이 새로운 분포를 t-분포라고 한다. 정규분포와 비슷하게 bell-shape을 가지고 있지만 꼬리부분이 훨씬 두텁다 (정규분포보다 extreme한 값이 나올 확률이 높다)

- 0을 중심으로 대칭적인 분포를 띤다
- 자유도(degree of freedom)이라는 하나의 모수는 가진다
cf. 정규분포는 2개의 모수(평균, 분산)를 가짐
- 자유도 작을수록 꼬리 부분이 두텁다
* 코시분포 Cauchy distribution
- t-분포이면서 자유도가 1인 분포
- 분산이 존재하지 않음
검정통계량
- 자유도가 n-1인 T-test statistic은 다음과 같이 정의된다

- point estimate : 내가 알고자 하는 모수의 추정값 (ex. 표본평균)
- null value : 귀무가설 하에서 모수 (ex. 13일 금요일 연구에선 0 ∵ 6일과 13일 교통량 차이 없다는 것이 귀무가설이니까)
- SE(=standard error) : 표준오차, 추정량(표본)의 표준편차
13일의 금요일 교통량 차이에 대한 가설 검정의 경우
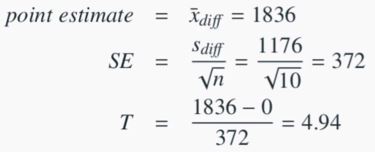
검정통계량과 p-value
- 이 경우 자유도는 n-1 = 10-1 = 9이다
- R을 이용한 계산

0에 대해 대칭이므로 pt(4.94, df=9, lower.tail=F) 와 pt(-4.94, df=9, lower.tail=T) 의 값은 같다.
lower.tail = T 이면 4.94 보다 작을 확률, lower.tail = F 이면 4.94보다 클 확률을 구해줌
귀무가설이 양측검정이기 때문에 2를 곱해줌
귀무가설이 교통량의 차이가 '다르다' 이므로 표본보다 실제 교통량이 클 경우 + 작을 경우 모두 구함
→ p-value가 매우 작기 때문에 귀무가설을 기각할 수 있다
13일의 금요일은 정말 불길한 날짜인가?
- p-value가 0.05보다 작기 때문에 교통량의 차이가 있다고 결론을 내릴 수 있다
- 실제로 차이가 어느 정도인지 알기 위해서 신뢰구간을 구해보자
2) 구간 추정치(신뢰구간)
신뢰구간
t-분포를 이용한 신뢰구간 공식은 다음과 같다


- R을 사용해 t*를 계산하면 t* = 2.26
- 따라서 모평균에 대한 95% 신뢰구간은 1836 ± 2.26 * 372 → (995, 2677)
- 그 전주 금요일과 비교했을 때, 13일의 금요일에 평균적으로 995-2677개의 차량이 덜 운행한다고 95% 확신한다
- 신뢰구간에 0이 포함되어 있지 않으므로 가설검정과 신뢰구간이 같은 결론을 내리고 있다
1) 가설검정의 결과 : 교통량에 차이가 있다
2) 신뢰구간의 결과 : 13일의 금요일에 교통량이 995-2677만큼 더 적다
* p-value 계산할 때 양측검정해야 하지만, 결론 내릴 때는 더 많다 /적다 (방향성) 얘기할 수 있다

11-2. 쌍체비교
Paired data에 관한 추론
읽기와 쓰기 시험
- 200명의 고등학생들의 읽기와 쓰기 능력에 대한 시험 결과는 다음과 같다

- 읽기와 쓰기 시험 점수는 서로 독립인가?
Paired data의 분석
- Paired data를 각 쌍의 차이를 이용하여 일 표본 문제로 분석한다
- diff = read - write
- 차이의 분포는 다음과 같다

1) 가설검정
- 귀무가설 : 평균적으로 개개인 고등학생의 쓰기와 읽기 점수의 차이는 없다
- 대립가설 : 평균적으로 개개인 고등학생의 쓰기와 읽기 점수의 차이가 있다. 즉 글쓰기와 읽기 능력은 별개이다.
T-검정
- diff의 표본평균 : -0.545
- 귀무가설에 따른 뮤 값 : 0
- 표본크기 n : 200
- 200명 학생의 표본표준편차 : 8.887

→ p-value가 크므로 귀무가설 기각 불가능
2) 신뢰구간
특별한 언급 없으면 95% 신뢰구간 사용

→ 신뢰구간에 0이 포함되므로 귀무가설 기각 불가능
예제 : 1루는 어떻게 돌아야 하나?
안타를 친 후 2루에 도달하기 위해서는 1루는 큰 각도로 돌아야 할까? 아니면 작은 각도로 돌아야 할까?
큰 각도로 돌면 가속도가 붙고 커브에 유리함. 작은 각도로 돌면 거리가 짧음


(작은 각도로 돌았을 때 걸린 시간) - (큰 각도로 돌았을 때 걸린 시간)
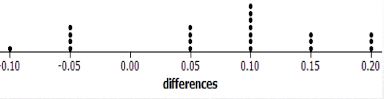
- 귀무가설 : 1루를 어떻게 도느냐는 2루에 도달하는 시간에 영향을 미치지 않는다
- 대립가설 : 1루를 어떻게 도느냐에 따라서 2루에 도달하는 시간은 달라진다
- diff = 작게 도는 각도의 기록 - 크게 도는 각도의 기록
(1) T-test
- 실제 실험에서는 1루를 크게 도는 경우 0.075초 빠른 것으로 나타났으며 표준편차는 0.088이었다
- 검정 통계량과 p-value는 다음과 같다

→ 따라서 1루를 크게 도는 게 2루에 도달하는 시간을 단축할 수 있다
- p-value를 구할 땐 양측검정을 하지만, 이는 p-value를 구하기 위함이고 결론을 내릴 땐 방향성을 제시할 수 있다
- p-value값이 작으므로 두 주루 방법에 "차이가 있음"을 알 수 있다
- 그런데 표본평균이 0.075로 양수이므로 크게 도는 것이 더 유리함을 알 수 있다(시간이 더 적게 걸림)
(2) Permutation test
- 만약 2가지 주루 방법에 차이가 없다면 사람별로 크게 도는 주루 기록과 작게 도는 주루 기록을 바꾼다고 해도 그 결과는 비슷해야 한다
- 이 경우 총 가능한 표본의 개수는 2^22 = 4,194,304이다 (22명의 학생에 대해 기록 2개 바꾸기 or 바꾸지 않기)
- 이 모든 경우를 다 고려할 수도 있지만 일반적으로 적당히 큰 횟수로 표본을 뽑아서 sampling distribution을 구한다
http://rossmanchance.com/ISIapplets.html
Applets for Introduction to Statistical Investigations
rossmanchance.com
- 22명 중 랜덤으로 주루 방법 바꾼 후 평균 diff를 구하는 시행을 1000번 반복
- 1000번의 permutation을 실시하여 sampling distribution을 뽑은 결과 다음과 같은 분포를 얻었다.
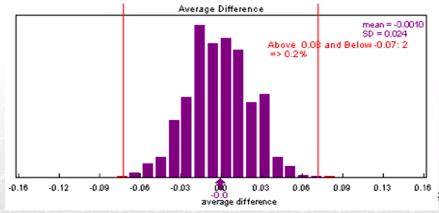
- 관측된 차이인 0.075보다 extreme한 경우를 관측할 확률은 0.02이다
- 사람별로 크게 도는 주루 기록과 작게 도는 주루 기록을 바꿔서 결과가 많이 달라짐. 따라서 2가지 주루 방법에 차이가 있다.
- 그런데 표본평균이 0.075로 양수이므로 크게 도는 것이 더 유리함을 알 수 있다(시간이 더 적게 걸림)
'stats' 카테고리의 다른 글
| 13. 분산분석 ANOVA (0) | 2020.01.11 |
|---|---|
| 12. 모평균에 관한 추론 II (0) | 2020.01.07 |
| 10. 중심극한정리와 검정력 (0) | 2020.01.07 |
| 9. Resampling과 가설검정 (0) | 2019.12.18 |
| 8. 통계적추론의 개요 (0) | 2019.12.18 |