2020. 1. 11. 21:23ㆍstats
SNUON 통계학
13-1. 3개 이상의 표본의 평균차이에 관한 추론
예제 : 강좌별 시험점수 비교
서울대 통계학과에서 이번 학기 통계학 교양 과목을 공대생 대상으로 3강좌를 제공한다. 강좌별로 중간고사 성적이 차이가 있는지 여부를 알고 싶다. 이 경우 적합한 가설검정은 무엇인가?
귀무가설 : 강좌별 중간고사 평균점수는 차이가 없다
대립가설 : 강좌별 중간고사 평균점수는 다르다
cf. 모집단 2개(Paired Data) : 두 평균의 차이가 0이냐 아니냐 문제로 해석
만약 3개 이상의 집단을 비교하고 싶다면?
- F-검정을 이용한 분산분석 ANOVA (Analysis of Variance)
- 분산분석을 하기 위한 3가지 조건
1) 각 그룹은 서로 독립이며 그룹 안의 관측치도 서로 독립이다
2) 각 그룹의 분산은 거의 같다 (퍼진 정도가 비슷)
3) 각 그룹의 분포는 정규성을 따른다 (아주 심각하게 skewed되지만 않는다면 큰 문제가 되지 않는다)
예제 : 강좌별 시험점수 비교
아래 그림에서 그룹 1,2,3을 비교해보아라. 그룹 간의 평균 점수의 차이가 있는지 시각적으로 알아볼 수 있는가?
그룹 4,5,6에 대해서도 비교해보아라.
- 그룹 1,2,3은 퍼진 정도(분산)에 큰 차이가 있어 보인다
- 그룹 4,5,6은 퍼진 정도(분산)가 큰 차이 없어 보인다
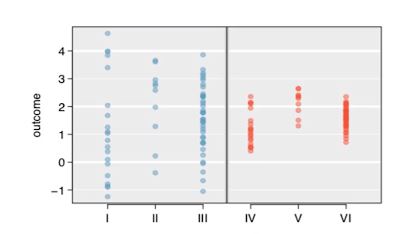
그룹간 변동 vs 그룹내 변동
- 그룹 1의 평균 = 그룹 4의 평균
- 그룹 2의 평균 = 그룹 5의 평균
- 그룹 3의 평균 = 그룹 6의 평균
- 하지만 왼쪽 그림에서 그룹 1,2,3의 평균 간의 차이가 있는지 알아보기 힘들다
- 반면에 오른쪽 그림에서 그룹 5의 평균이 다른 그룹에 비해 높아보인다
- 그룹 간의 변동이 그룹내의 변동보다 상대적으로 커야 그룹 간 평균의 차이를 탐지할 수 있다
예제 : 메이저리그 선수들의 출루율
일반적으로 야구선수들은 포지션에 따라서 타격성적의 차이가 있다고 알려져 있다. 이 가설을 검증하기 윟 2010년 MLB 선수들의 포지션 (지명타자, 내야수, 외야수, 포수)별로 평균 출루율이 차이가 있는지 알아보자
( 단,2010년도 총 200 타수 이상을 기록한 327명의 선수를 대상으로 타격기록을 조사하였다.)
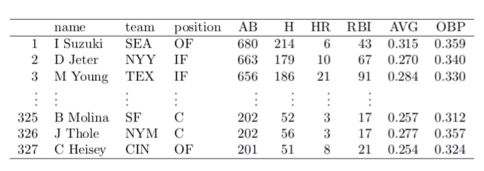
AB : 타수
H : 안타
OBP : 출루율
포지션별 summary statistics
| 외야수 OF | 내야수 IF | 지명타자 DH | 포수 C | |
| 표본크기 | 120 | 154 | 14 | 39 |
| 표본평균 | 0.334 | 0.332 | 0.348 | 0.323 |
| 표본분산 | 0.029 | 0.037 | 0.0360 | 0.045 |
포지션별 side-by-side boxplot
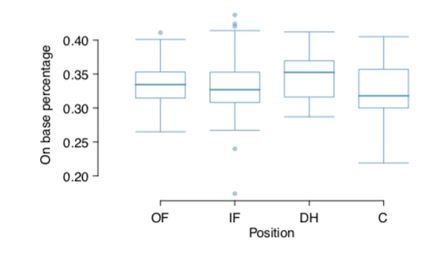
가설검정
- 귀무가설 : 포지션에 상관없이 평균 출루율이 같다 (뮤OF = 뮤IF = 뮤DH = 뮤C)
- 대립가설 : 포지션별로 평균 출루율의 차이가 있다 (최소 두 그룹끼리는 차이가 있다)
- 앞의 side-by-side boxplot을 관측한 결과, 지명타자 그룹과 포수 그룹 간의 평균 출루율의 차이가 크게 나는 것처럼 보인다. 그렇다면 "뮤DH = 뮤C"로 가설검정을 하면 어떨까?
- 여러 그룹을 비교 시 눈으로 미리 모든 자료를 비교한 후 (즉 side-by-side boxplot을 관측한 후) 어느 그룹들을 비교할 지 결정하는 것은 적절치 않다!
- 위와 같은 방식을 data fishing 혹은 data snooping이라고 한다
* 눈으로 확인, 또는 summary stats만 보고 임의로 두 집단 뽑아 두 집단만 비교하는 것은 위험하다
Data Fishing / Snooping
- 초등학생들의 학습능력을 평가하고자 한다. 20개 학급에 학생들을 임의로 배정한 후 바로 학습능력을 테스트 한 다음 학급별 점수를 살펴보자
- 임의배정에 의해서 학급별 평균점수차이는 유의미하지 않아야 한다
- 하지만 비교대상이 많은데도 불구하고 임의로 가장 차이가 나는 두 학급만 선정하여 평균정수는 t-test를 이용해서 가설검정을 한다면 두 학급의 평균점수는 차이가 난다고 결론을 내릴 수 있다
ANOVA와 F-검정
변동의 분할
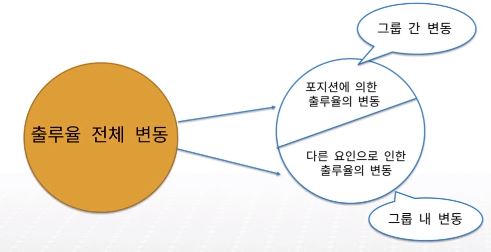
데이터의 구조

n_i = 그룹 i의 데이터 개수
x_ij = i번째 그룹의 j번째 데이터
변동의 분할

x̄ = 모든 그룹의 평균 (총 평균)
x̄_i = i 그룹의 평균
총 변동 SST는 SSE와 SSG로 나누어진다 ( 변동 = 그룹 간 변동 + 그룹 내 변동)
SST = (그룹에 관계없이) 총 분산
SSG = 그룹 간의 변동 (각 그룹의 평균과 총 평균의 차를 제곱한 것의 총 합)
SSE = 그룹 내 변동
K 그룹의 비교

df_E = degree of freedom = 자유도 = (n-k)
* 평균이 k개 있으니 n에서 k 뺀 것이 자유도
* 분산 계산할 때 (n-1)로 나눈 것과 유사
df_G = (k-1)
* 그룹의 개수 k개, 전체 평균 값은 1개 이므로 (k-1)
F 검정
- 귀무가설 하에서 검정통계량은 F(k-1, n-k) 분포를 따른다
- 출루율 예제에서 k-1 = 4-1 = 3, n-k = 327-4 = 323
<분산분석표>
| 자유도 | Sum of Square | Mean Square | 검정통계량 | P-value | |
| 그룹 | 3 | 0.0076 (SSG) | 0.0025 (MSE) | 1.9943 (MSG/MSE) | 0.1147 |
| 잔차 (그룹 내 변동) | 323 | 0.4080 (SSE) | 0.0013 (MSG) |
F(3,323)의 분포

p값 > 0.05
따라서 귀무가설을 기각할 수 없다
Q. 왜 단측검증을 했는가?
변동(제곱해서 계산)으로 계산했기 때문에 양수밖에 나올 수 없다. 따라서 검정통계량은 항상 양수
F 검정을 위한 가정 CHECK
- 독립성 : 데이터가 전체 모집단의 10% 이내로 simple random sample로 뽑혔다면 독립성이 성립한다고 가정
- 정규성 : 각 그룹별 normal probability plot을 이용하여 check
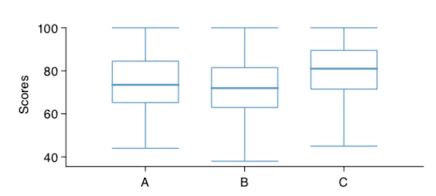
- 등분산성 : side-by-side boxplot을 이용하여 각 그룹별 데이터의 퍼진 정도를 비교
정규성 검정
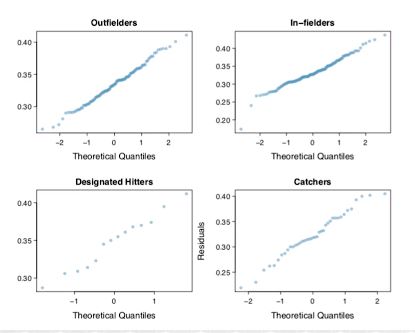
등분산성 검정

13-2. 다중비교
다중비교 (Multiple Comparisons)
- 국회의원 선거에서 95% 신뢰구간을 이용해서 실제 당선자의 숫자를 예측한다고 생각해보자
- 편의상 200명의 선거구가 있다고 가정하면 95% 신뢰구간 안에 참값이 포함되지 않는 경우가 평균적으로 10개가 있다. 즉 여러 개의 선거구 결과를 동시에 예측한다면 평균적으로 10개는 틀리는 것이다!
예제 : 통계학 강좌 별 중간고사 성적 비교

R의 분산분석표

- F 검정의 결과 강좌 별 평균의 차이가 있다고 말할 수 있다 ( p값 < 0.05 이므로)
- 그렇다면 차이가 있는 강좌는 무엇인가?
Bonferroni correction
- F 검정을 통해 그룹별로 평균의 차이가 있다고 결정한다면 그룹 간의 비교를 고려할 수 있다. 이때 가능한 총 비교의 수는 M = k (k-1)/2 = k C 2 (조합)
* k = 그룹의 개수
- 이 경우 비교시 사용해야 할 유의수준은 a* = a / M
* 여러 테스트를 동시에 하면 95% 신뢰구간 이용 / 유의수준 0.05 쓰면 10개 오류(선거구 예제). 따라서 새로운 유의수준 필요!
통계학 강좌 중간고사 예제의 경우
- F 검정의 결과 강좌 별 평균점수의 차이가 있다
- 강좌 A와 B, B와 C, C와 A의 그룹 간의 평균의 차이를 비교하는 t-검정을 실시하자
- 즉, 총 비교의 개수는 3 = 3*2/2 이며 각 검정에서의 유의수준은 0.05/3 = 0.0167을 사용한다
강좌별 비교결과
- 강좌 A와 B의 평균 차이에 대한 검정결과 p-value는 0.228
- 강좌 B와 C의 평균 차이에 대한 검정결과 p-value는 0.1462
- 강좌 C와 A의 평균 차이에 대한 검정결과 p-value는 0.0102
강좌 C와 A의 평균 차이에 대한 검정결과 p-value가 0.0167보다 작기 때문에 귀무가설을 기각한다. 즉 강좌 A와 C의 중산고사 평균점수의 차이가 존재한다.
※ F 검정을 기각했는데 , 그룹별 t-검정을 하면 차이가 안 나오는 경우 : 그룹 별 차이가 있긴 있는데 어디서 차이가 나는지 탐지할 수 없는 경우
'stats' 카테고리의 다른 글
| 15. 모비율에 관한 추론 II (0) | 2020.01.14 |
|---|---|
| 14. 모비율에 관한 추론 I (0) | 2020.01.12 |
| 12. 모평균에 관한 추론 II (0) | 2020.01.07 |
| 11. 모평균에 관한 추론 I (0) | 2020.01.07 |
| 10. 중심극한정리와 검정력 (0) | 2020.01.07 |