2020. 1. 7. 23:01ㆍstats
SNUON 통계학
Inference for Numerical Data
1. 일 표본평균과 t-분포
2. Paired data에 관한 추론
3. 두 표본평균의 차이에 관한 추론
4. Power Analysis
5. ANOVA
12-1. 두 표본의 평균 차이에 관한 추론
예제 : 다이아몬드
- 다이아몬드의 무게는 캐럿으로 표기한다
- 1캐럿은 100point라고 한다면 0.99캐럿은 99점이다
- 사람의 눈으로 1캐럿과 0.99캐럿은 구별할 수 없지만, 1캐럿의 가격이 0.99캐럿의 가격보다 훨씬 비싸지 않을까?
- 이 경우 양측검정을 사용해야 할까? 아니면 단측검정을 사용해야 할까?

가설검정
- 귀무가설 : 0.99캐럿과 1캐럿 다이아몬드의 가격이 같다
- 대립가설 : 1캐럿이 0.99캐럿 다이아몬드보다 비싸다 (1캐럿이 0.99보다 쌀 가능성은 없다고 보고 단측검정)
CLT(중심극한정리)를 적용하기 위한 조건
- 각각의 표본이 30이상이다
- 각각의 표본의 분포가 skewed하지 않다
- 두 개의 그룹이 서로 독립이다
위의 조건을 만족하는 경우 귀무가설 하에서

- 하지만 다이아몬드 예제에서 0.99캐럿은 23개뿐이다!
- 이 경우 test statistic은 (근사)자유도가 다음과 같은 t분포를 따른다

- 위의 자유도는 일반적으로 정수가 아니다
- 따라서 컴퓨터로 계산하지 못한다면, 아래 방법을 추천한다

- 자유도가 작아야 안전함 (보수적인 방법)


-2.508이라는 값은 자유도에 따라 p-value가 달라진다
- 자유도는 근사식으로는 45.26, 둘 중 최솟값을 선택하는 간편한 방법을 사용하면 22가 나온다
- 자유도가 실제보다 큰 경우 p-value는 더 작아진다
- 자유도가 실제보다 작은 경우 p-value는 더 커진다

- p-value가 0.05보다 작으므로 귀무가설을 기각할 수 있다
- 1캐럿의 평균 가격이 0.99캐럿의 평균 가격보다 비싸다 (T값이 마이너스니까)
두 집단의 분산이 같은 경우
- 만약 두 모집단의 분산이 같은 경우 어떻게 될까?
- 이 경우는 다음과 같은 test statistic을 사용한다

- 여기서 sp는 다음과 같다

- 귀무가설하에서 검정통계량의 분포는 자유도가 ( n1 + n2 - 2 ) 인 t-분포를 따른다
∵ (n1-1) + (n2-1) = (n1 + n2 -2)
만약 다이아몬드 예제에서 두 집단(0.99캐럿과 1캐럿의 가격)의 분산이 같다면 검정통계량은 다음과 같다.

- 자유도는 23 + 30 -2 = 51이며, p-value는

- p-value가 0.05보다 작으므로 귀무가설을 기각할 수 있다
정리 : 두 표본의 비교
1) 두 집단의 표본의 크기가 각각 30이상일 경우 : CLT를 적용할 다른 조건을 확인한 후 test statistic이 정규분포를 따른다는 가설하에 가설검정을 한다
2) 두 집단의 표본의 크기가 작은 경우 (즉 최소 한 표본의 크기가 30미만인 경우)
- 두 모집단의 분산이 같은 경우
- 두 모집단의 분산이 다른 경우
- 분산의 크기가 같은지 여부를 F-검정을 통해 알 수 있다. 그러나 이 경우 표본의 크기가 작기 때문에 F-검정을 사용하면 검정력이 현저히 떨어진다. 따라서 선행연구 혹은 과학적 근거에 의해 분산이 같은지 여부를 가정한다
(일반적으로 분산이 같음을 증명하기 어려우므로 분산이 다르다고 가정하고 검정을 진행한다)
Permutation test
- 가능한 Permutation test는?
귀무가설 : 0.99캐럿과 1캐럿 다이아몬드의 가격이 똑같다
0.99캐럿, 23개 + 1캐럿, 30개 = 총 53개
53개의 다이아몬드 중 임의로 23개를 뽑아 0.99캐럿의 가격표를 붙임. 나머지는 1캐럿의 가격표를 붙임
이에 따른 히스토그램을 그려 우리가 관측한 값이 얼마나 extreme한지 보면 됨
Tukey's Quick Test
- 두 집단 간의 차이가 통계적으로 유의미한지 확인하기 위해 우리는 2 sample t-test를 일반적으로 사용한다
- 하지만 컴퓨터나 계산기 등을 사용하지 않고 쉽게 두 집단의 차이 여부를 통계적으로 검증할 수 있을까?
- Tukey의 quick test는 이러한 경우를 염두에 두고 제안되었다
x = 높은 그룹에서 낮은 그룹의 최댓값보다 큰 숫자 + 낮은 그룹에서 높은 그룹의 최솟값보다 작은 숫자 (겹치지 않는 부분)
x > 7이면, 유의수준 α = 0.05에서 기각
x > 10이면, 유의수준 α = 0.01에서 기각
x > 13이면, 유의수준 α = 0.001에서 기각
tie가 있다면 1/2로 간주한다
※ 주의사항
- 두 집단의 크기가 너무 차이가 나지 않아야 한다 (4:3 정도의 비율까지 가능)
- 각 집단의 크기가 30보다 작아야 한다
예제 : 중고 카메라
만약 중고카메라를 친구로부터 산다면 모르는 사람에게서 구입할 때와 똑같은 가격으로 구입할까?
귀무가설 : 친구에게서 살 때랑 모르는 사람에게서 살 때랑 가격이 같다
| 친구에게서 구입 | 모르는 사람에게서 구입 |
| 275 | 260 |
| 300 | 250 |
| 260 | 175 |
| 300 | 130 |
| 275 | 200 |
| 290 | 225 |
| 300 | 240 |
| 255 |
모르는 사람에게서 구입한 경우가 낮은 그룹, 친구에서 구입한 경우가 높은 그룹
- 낮은 그룹의 최댓값은 260. 높은 그룹에서 260보다 큰 자료의 개수는 6개, 260과 같은 자료의 개수는 1개 (1/2)
- 높은 그룹의 최솟값은 255. 낮은 그룹에서 255보다 작은 자료의 개수는 6개
따라서 x = 6.5 + 6 = 12.5
p-value를 0.01과 0.001 사이로 간주할 수 있다
12-2. 검정력 분석
* 검정력 증가 = 제 2종오류 감소
예제 : 고혈압 치료약
- 제약회사에서 고혈압 치료약의 효능을 검증하기 위해 임상실험을 하려고 한다
- 고혈압 환자 200명을 피실험자로 구한 후 randomizatin을 통해서 실험군(신약 사용)과 대조군(기존의 고혈압 약 사용)으로 나눈다
- 두 집단 간의 평균 고혈압 차를 구한다
- 선행연구를 통해 고혈압 환자들의 혈압 수치의 표준편차는 12로 알려져 있다고 가정
- n1 = n2 = 100
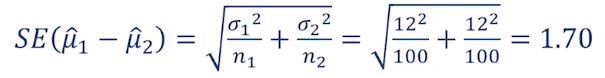
- 두 평균의 차이가 1.96 * SE = 1.96 * 1.70 = 3.332보다 크면 유의수준 α = 0.05에서 귀무가설을 기각한다
(귀무가설 : 두 약의 효과에 차이가 없다)
검정통계량 = 두 집단 평균의 차이 ÷ SE
P ( 검정통계량 > 1.96 ) = P ( 두 집단 평균의 차이 ÷ SE > 1.96 ) = P ( 두 집단 평균의 차이 > 1.96 * SE ) = P ( 두 집단 평균의 차이 > 3.332)

- 대립가설이 참이라면 위의 확률을 검정력(Power)으로 간주할 수 있다

- 델타 = -3 이라 가정 : 신약이 고혈압을 3 정도 떨어뜨린다는 의미
- 대립가설 하에 이런 결과를 관측할 확률이 42%이다 (=검정력이 42%)
- 일반적으로 검정력 70% 이상
- 표본크기를 늘리면 검정력이 높아진다
n1 = n2 = n이고 델타= -3이라고 가정할 경우, 검정력이 0.8이 되기 위한 표본크기는 얼마인가?

- 따라서 검정력이 최소 80%가 되려면 표본크기는 251이상이어야 한다
- 만약 검정력을 증가하려면 (1) 표본크기를 크게 하거나, (2) 유의수준을 높이거나, (3) 표준편차를 줄여야 한다
* (2) 유의수준을 높이면 1종 오류가 많아짐
'stats' 카테고리의 다른 글
| 14. 모비율에 관한 추론 I (0) | 2020.01.12 |
|---|---|
| 13. 분산분석 ANOVA (0) | 2020.01.11 |
| 11. 모평균에 관한 추론 I (0) | 2020.01.07 |
| 10. 중심극한정리와 검정력 (0) | 2020.01.07 |
| 9. Resampling과 가설검정 (0) | 2019.12.18 |