2020. 1. 12. 14:47ㆍstats
SNUON 통계학
범주형 자료의 추론
1. 일표본비율에 관한 추론
2. 이표본비율의 차이에 관한 추론
3. Goodness of fit test와 카이제곱 분포
4. 분할표에서 독립성 검정
5. 소표본에서 표본비율에 관한 검정
6. 역학 (epidemiology) 에서 2*2 분할표 분석
14-1. 단일표본 비율에 관한 추론
표본비율이 정규분포를 따를 조건
- 한국 갤럽에서 2019년 1월 미세먼지 나쁨 예보 발령 시 마스크의 착용 여부에 대한 여론조사를 실시하였다. 1000명의 조사대상자 중 53%가 마스크를 착용한다고 대답하였다
- 여기서 응답자가 마스크를 착용한다고 한 경우를 1, 그렇지 않은 경우를 0이라고 하자. 이 경우 표본비율은 0과 1로 이루어진 응답들의 평균이다.
* 0과 1로만 이루어진 확률변수 (binary) = 베르누이 확률변수
p = 0 + 1 + 1 + ... + 0 / 976 = 0.53
* 실제 응답자 = 976
- 따라서 아래의 조건을 만족할 경우 중심극한정리를 사용하여 표본비율이 정규분포를 따른다고 할 수 있다
1) 표본 관측치들이 서로 독립이다
2) np >= 10 && n(1-p) >= 10 을 만족한다 (*여기서 p는 표본비율 p^)
- 원래 CLT의 조건은 표본크기가 30 이상이지만 모집단의 분포가 skewed 되어 있는 경우 (즉, 모비율 p가 0이나 1에 근접한 경우) 표본크기가 좀 더 커져야 한다는 걸 반영
- 주어진 2가지 조건을 만족하는 경우 : 표본비율이 다음과 같은 정규분포를 따른다
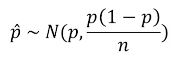
- 1번째 독립성 조건은 표본의 크기가 전체 모집단 크기의 10% 이내로 simple random sample로 뽑힌 경우 성립한다고 본다
- 2번째 조건에서 모비율 p를 모르기 때문에 표본비율 혹은 가설검정의 경우에는 p의 null value가 사용된다
표본비율의 신뢰구간
- 신뢰구간의 일반적인 공식은 Point Estimate ± Z*SE
- 하지만 표본비율의 SE는 모비율 p에 의존한다



예제 : 비상사태시 병동폐쇄에 관한 여론조사
MERS와 같은 비상상태가 발발시 병동폐쇄에 관한 서울시민의 찬반여부를 조사하였다. 총 1024명이 설문조사에 응답하였고, 이 중 찬성하는 비율은 82%였다. 모비율 p의 95% 신뢰구간을 구하여라
- 독립성 가정은 만족한다고 할 수 있다
- 먼저 중심극한 정리를 적용할 수 있는지 조건을 체크하자
np = 1024 * 0.82 = 854.21 >= 10
n(1-p) = 1024 * 0.18 = 187.79 >= 10
따라서 모비율에 관한 95% 신뢰구간은

우리는 서울 시민 중 메르스와 같은 비상사태 시 병동폐쇄를 판성하는 비율이 79.6% 에서 84.4% 사이에 있다는 것을 95% 확신한다
모비율에 관한 가설검정
- 귀무가설 : p = p_0
- 대립가설 : p != p_0

* 신뢰구간 구할 때의 SE와 검정통계량에서 사용한 SE가 다르다!
모비율에 관한 가설 검정
비상사태에 관한 여론 조사에서 p_0 = 0.7이라고 가정하자. 유사한 질병에 관한 여론조사를 참조해서 일반적으로 이러한 전염병에 대한 인식을 기준으로 선정했다고 하자. 메르스에 대해 p_0 = 0.7 인지 가설검정을 통해 확인해보자.

검정통계량의 값이 1.96보다 훨씬 크므로 유의수준 0.05에서 귀무가설을 기각한다
즉, 찬성비율이 0.7과 다르다고 할 수 있다
Sample size calculation
- 오차범위 (margin of error)가 주어진 경우 sample size를 구해보자
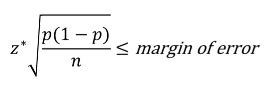
- 여기서 p는 선행연구의 결과를 이용하거나 (일반적으로) p = 1/2 을 사용한다.
* p = 1/2일 때 최댓값
예제 : 대학신문사 여론조사
대학신문이 수강신청 변경기간을 수업일수 1/4로 줄이는 것에 관한 여론조사를 실시하였다. 95% 수준에서 오차범위가 0.04보다 작게 하려면 표본의 개수를 최소 얼마 이상으로 해야 하나?
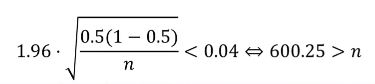
즉, 표본크기는 601명 이상이어야 한다
14-2. 두 표본의 비율 차이에 관한 추론
예제 : 대학축제와 주류판매
대학축제와 주류판매를 허용해야 되는지 여부에 대해 일반인과 대학생들에게 설문조사를 실시하였다. 결과는 다음과 같았다.
| 주류판매 찬성 | 주류판매 반대 | 총 | |
| 일반인 | 362 | 409 | 771 |
| 대학생 | 249 | 483 | 732 |
일반인과 대학생들의 주류판매 허용여부에 대한 찬성비율이 같은가?
Sampling distribution of p1 - p2
- 두 집단에서 모비율을 p1, p2이라 하고 표본의 크기를 n1, n2라고 하자
- 만약 두 집단이 독립성과 아래, 조건을 만족하면
n1p1 >= 10, n1(1-p1)>=10, n2p2>=10, n2(1-p2)>=10
- 중심극한정리에 의해서 (p1-p2) 가 다음과 같은 정규분포를 따른다

- 따라서 (p1-p2)의 표준편차(표본오차)는 다음과 같다

p1 - p2의 신뢰구간
- 대학축제 주류판매 예제에서 p1-p2 의 95% 신뢰구간을 구해보자
- 신뢰구간 공식 = point estimate ± z * SE
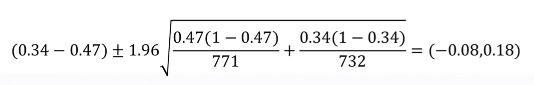
- p1-p2 의 신뢰구간이 0을 포함함. 따라서 귀무가설을 기각할 수 없다.
- p1과 p2과 다르다고 볼 수 없다
p1-p2의 가설검정
- Mammogram이 실제로 유방암 예방에 도움이 되는지 알아보자
- 30년 동안 약 9만명의 여성을 대상으로 mamogram과 다른 유방암 검사를 받게한 후 실제 유방암으로 사망한 숫자를 비교해 보았다.
| 사망 | 생존 | 총 | |
| Mammogram | 500 | 44,425 | 44,925 |
| Control | 505 | 44,405 | 44,910 |
Mammogram이 다른 검사에 비해 효과적이었나?
- 귀무가설 : p1 = p2
- 대립가설 : p1 != p2
귀무가설하에서 SE(p1-p2) 는?
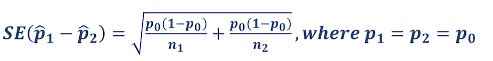
p0는 어떻게 추정? 전체 평균 (두 집단으로 나눈 것 상관없이 전체 평균)

- 먼저 p0 = 1005 / 89830 = 0.0112
- CLT 조건 확인
n1 * p0 >= 10 , n1 * (1-p0) >= 10 , n2 * p0 >= 10 , n2 * (1-p0) >= 10
- SE(p1-p2)
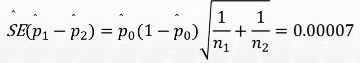
- 검정통계량은
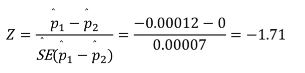
- p-value는 P ( |Z| > 1.71 ) = 0.08
- 귀무가설을 기각할 수 없다. Mammogram과 기존 검사 결과의 차이가 있다고 할 수 없다
14-3. 적합성 검정과 카이제곱 분포
Weldon's dice
- Weldon은 1894년 12 dice를 26,306번 던져서 그 중 5 또는 6이 나온 경우를 성공으로 간주하고 성공의 횟수를 기록했다
- 이 실험에서 성공의 횟수는 전체 횟수의 1/3보다 많이 나왔다. 피어슨은 그 이유로 싸구려 주사위의 경우 주사위 눈을 만들기 위해 눈을 파내면서 각 면의 무게가 차이가 났고 그 결과 가장 무거운 1 또는 2가 있는 면이 보다 많이 바닥에 닿았고, 따라서 5 또는 6이 많이 관측되었을거라는 가설을 제기하였다
Labby's dice
- Weldon의 실험을 일주일 만에 재현할 수 있었다
- 하지만 Labby는 Weldon이 관측했던 현상 (5와 6이 기대이상으로 많이 나오는 현상)을 재현하지 못했다.
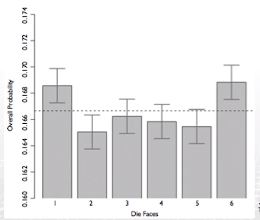
- Labby는 각 눈이 나오는 횟수를 다음과 같이 기록하였다
Setting the hypotheses
실제 관측자료와 기댓값의 차이가 있다고 확신할 수 있는가?
- 귀무가설 : 기댓값과 관측치 사이의 불일치는 없다. 관측치와 기댓값은 같은 분포를 따른다
- 대립가설 : 관측치와 기댓값이 일치하지 않는다. 관측치와 기댓값은 다른 분포를 따른다. 즉 주사위의 결과가 실제로 공정하게 각 눈을 보여주지 않는다
(주사위 눈 확률이 1/6 씩이 아니다!)
- 주사위 총 10번 던져서 짝수가 6번 나오면, 기댓값과 관측치의 차이가 1
- 주사위 총 1000번 던져서 짝수가 512번 나오면, 기댓값과 관측치의 차이가 12
- 절대적 수치로만 따지면 총 시행횟수 늘릴수록 기댓값과 관측치의 차이가 벌어질 수밖에 없다
- 따라서 전체 시행횟수를 고려해서 표준화해야 함
Evaluating the hypotheses
- 이 가설을 검정하기 위해서 우리는 실제 관측치와 기댓값의 차이가 얼마나 큰지 판단하는 근거를 제시해야 한다
- 차이가 클수록 이 차이는 sampling variation으로 인해 우연히 발생한 것이라기 보다는 대립가설이 참일 가능성이 높다
- 여기서 우리는 실제 자료가 예상한 분포에 얼마나 적합한지를 알아보고 있기 때문에 이러한 검정을 적합도 검정(goodness of fit)이라고 한다
Anatomy of a test statistic
- 일반적인 검정통계량(test statistic) = [ point estimate - null value ] / SE of point estimate
* point estimate = 관측치, null value = 기댓값
- 위의 검정통계량 공식은 다음과 같은 2가지에 바탕을 둔다
1) 귀무가설하에서 추정치와 기댓값의 차이 계산
2) 차이를 추정치의 표본오차로 나누어 표준화
- count data에서도 위의 아이디어를 적용하여 검정통계량을 제안할 수 있다
Chi-square statistic
- 실제 관측된 갯수와 기댓값의 차이를 이용해 다음과 같은 검정통계량을 제시할 수 있다
- x^2 statistic

- 포아송 분포는 평균=분산. 관측치가 평균=분산=E인 포아송 분포를 따른다면
O - E / √ E → (상쇄하는 것을 없애기 위해) 전체 제곱 → (O-E)^2 / E
Calculating the chi-square statistic
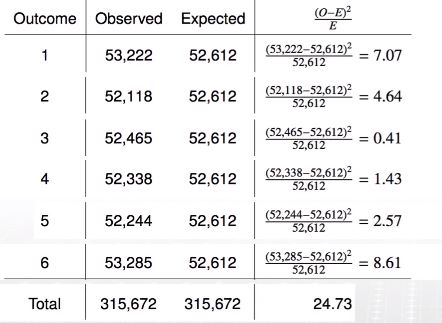
24.73이라는 값이 얼마나 큰지 (혹은 작은지) 알아보려면 어떤 분포를 따르는지 알아야함 !
: 카이제곱분포를 따른다
Why square? 차이의 제곱을 사용하는 이유
1) 차이가 항상 양수가 된다
2) 절댓값을 사용하는 경우 검정통계량의 분포를 구하는 것이 일반적으로 쉽지 않다
The chi-square distribution
- 검정통계량이 실제로 얼마나 큰지 여부를 판단하기 위해서 먼저 x^2 분포에 대해 알아보자
- 카이제곱분포의 모수는 degree of freedom (df) 하나이다. 이 모수가 분포의 형태, 중앙, 퍼진 정도에 영향을 준다

Practice

자유도가 증가함에 따라서
1) 카이제곱분포의 center도 증가한다
2) 카이제곱분포의 variability도 증가한다
2) 카이제곱분포의 shape는 정규분포와 닮아진다
Finding areas under the chi-square curve
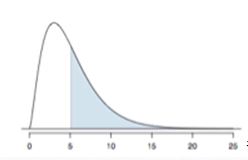
p-value = tail area under the chi-square distribution
(F-분포와 마찬가지로 제곱했으니 한 쪽만 생김)
Finding the tail areas using R
pchisq(q=30, df=10, lower.tail=F)
# 0.0008566412
Back to Labby's dice
- Labby의 실험결과가 주사위가 공정한 주사위인지 여부를 확인해주는가?
- 귀무가설 : 기댓값과 관측치 사이의 불일치는 없다. 관측치와 기댓값은 같은 분포를 따른다
- 대립가설 : 관측치와 기댓값이 일치하지 않는다. 관측치와 기댓값은 다른 분포를 따른다. 즉 주사위의 결과가 실제로 공정하게 각 눈을 보여주지 않는다
- 검정통계량 x^2 = 24.67
Degrees of freedom for a goodness of fit test
- 이 경우 귀무가설 하에서 검정통계량의 분포는 카이제곱분포를 따라가며 자유도는 다음과 같다
df = k-1
- Labby의 실험의 경우 자유도는 다음과 같다
df = 6-1 = 5
R
pchisq(q=24.67, df=5, lower.tail=F)
# 0.00161338
- p-value가 0.05 보다 작기 때문에 귀무가설 기각할 수 있다
- 유의수준 0.05에서 귀무가설을 기각한다. 즉 실험에 사용된 주사위는 공정한 주사위라고 할 수 없다
결과
- 1-6 쌍이 2-5 또는 3-4보다 훨씬 많이 나온다
- Pearson의 주장은 이 실험자료에 의해서 뒷받침된다고 하기 힘들다
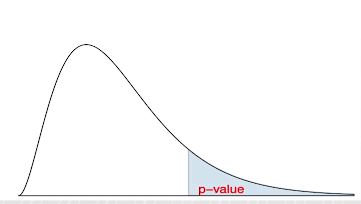
요약 : p-value for a chi-square test
- 검정통계량의 p-value는 검정통계량보다 큰 값의 영역을 의미한다
- F검정과 마찬가지로 검정통계량은 항상 양수이기 때문에 검정통계량의 값이 클수록 강한 증거를 의미한다
Conditions for the chi-square test
- Independence : 각각의 경우가 서로 독립니다
- Sample size : 각 경우마다 기댓값이 적어도 5 이상이어야 한다
- df > 1 : 자유도가 1보다 커야 한다
'stats' 카테고리의 다른 글
| 16. 회귀분석 I (0) | 2020.01.15 |
|---|---|
| 15. 모비율에 관한 추론 II (0) | 2020.01.14 |
| 13. 분산분석 ANOVA (0) | 2020.01.11 |
| 12. 모평균에 관한 추론 II (0) | 2020.01.07 |
| 11. 모평균에 관한 추론 I (0) | 2020.01.07 |