2020. 1. 15. 15:25ㆍstats
SNUON 통계학
선형회귀분석
1. 직선적합, 잔차, 상관관계
2. 최소제곱추정법
3. 이상점
4. 회귀분석의 추론
16-1. 직선적합, 잔차, 상관관계
1) 범주형 변수 하나, 연속형 변수 하나 : 분산분석
(ex) 각 반의 평균 비교
2) 범주형 변수 두개 : 분할표
(ex) 카이제곱 검정 (독립성/동일성 검정)
3) 연속형 변수 두개 : 선형회귀분석
Modeling numerical variables
두 연속변수 사이의 관계를 모형화하는 방법을 배우고 특히 한 변수를 이용하여 다른 변수를 예측할 경우에 대해서 알아보자
Poverty vs. HS graduate rate
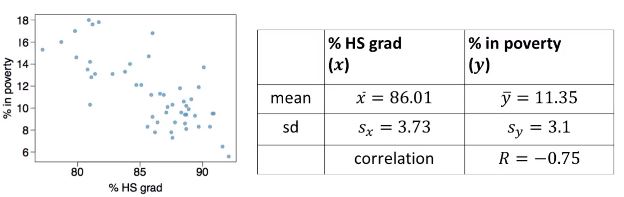
아래 scatterplot (산점도)는 미국 50개 주와 DC에서 고등학교 졸업률과 빈곤율 사이의 관계를 보여준다

- 반응변수는? 빈곤율
- 설명변수는? 고등학교 졸업률
- 두 변수 사이의 관계는? 음의 상관관계 (반비례 관계)
Quantifying the relationship
- 상관계수(correlation)는 두 연속형 변수 사이의 선형(linear) 관계의 정도를 나타내는 측도
- 상관계수는 1(perfect positive)과 -1(perfect negative) 사이의 값을 가진다
- 상관계수가 0인 경우 선형관계가 전혀 없다는 것을 의미한다
- 두 변수가 선형관계가 아니라면, 상관계수 필요없음!
상관관계 공식
- 상관계수(correlation)의 정의는 다음과 같다

- 여기서 Cov(X,Y) = E(XY) - E(X)*E(Y)
* 기하학적 해석 : corr = 코사인 θ ( X,Y 완벽 일치하는 경우 코사인 0 = 1 )
- 표본상관계수는 다음과 같이 계산할 수 있다

16-2. 최소제곱추정법 Fitting a line by least squares regression
잔차(Residual)
- 모형 적합 후 실제 값과 적합된 모형의 차이
- Data = Fit + Residual

- 잔차 e_i

* y_i = 실제 데이터, y_i_hat = 예측치
- DC의 빈곤율은 예측치보다 5.44% 높다
- RI의 빈곤율은 예측치보다 4.16% 낮다

A measure for the best line
- 잔차가 작을수록 직선 적합이 잘 되었다고 생각할 수 있다
1) 잔차의 절댓값을 최소화
2) 잔차의 제곱을 최소화 (least squares)
- 최소제곱법을 사용하는 이유?
1) 가장 일반적
2) 손으로 계산하기 쉽고 모든 통계 프로그램에서 구현되어 있음
3) 잔차의 값이 2배라는 것은 실제 상황에서는 그 이상으로 나쁜 경우가 종종 있기 때문에 제곱이 이 상황을 잘 반영한다
The least squares line
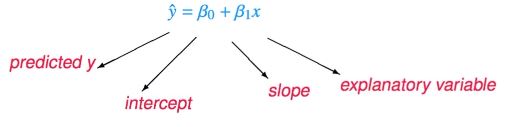
- 절편(Intercept) : Parameter = β_0 / Point estimate = b0
- 기울기(Slope) : Parameter = β_1 / Point estimate = b1
( β 가 모집단의 값, b는 샘플(표본)로 추정한 값)
R output
Slope
- 회귀직선의 기울기는 다음과 같이 주어진다

- 빈곤율과 고교졸업률의 예제에서 b1 = 3.1 / 3.73 * (-0.75) = -0.62
- 해석 : 고교졸업률이 1% 높아지면 평균적으로 빈곤율이 0.62% 낮아질 것으로 예상된다
Intercept
- 절편은 회귀직선에서 x=0일 때 y의 값이다. 절편의 공식은 회귀직선이 (x bar, y bar) 를 지난다는 점을 착안하면 다음과 같이 주어진다

- 빈곤율과 고교졸업률의 예제에서 b0 = 11.35 - (-0.62)*86.01 = 64.68
- 해석? : 고교졸업률이 0% 일 때 빈곤율이 64.68%로 예상된다 ( 사실상 의미 X )
- x=0 이라는 의미는 고교졸업률이 0이라는 걸 의미하지만 실제로 그러한 주는 없을 것으로 생각되며, 또한 대부분 졸업률이 0보다 훨씬 높기 때문에 절편값 자체에 대해 큰 의미를 두지 않는다
Interpretation of slope and intercept

- Intercept : x=0일 때, y의 값
- Slope : x가 1단위 증가할 때, y는 평균적으로 기울기만큼 증가/감소한다
※ 주의 : 자료가 randomized controlled experiment에서 얻어진 것이 아니라면 위의 해석은 인과관계를 의미하는 것은 아니다
Prediction
- 회귀분석모형을 이용하여 주어진 설명변수 값에 대응하는 반응변수의 값을 추정하는 것을 예측(prediction)이라고 한다
- 이러한 예측치에는 불확실성이 동반된다
'stats' 카테고리의 다른 글
| 18. 회귀분석 III (0) | 2020.01.15 |
|---|---|
| 17. 회귀분석 II (0) | 2020.01.15 |
| 15. 모비율에 관한 추론 II (0) | 2020.01.14 |
| 14. 모비율에 관한 추론 I (0) | 2020.01.12 |
| 13. 분산분석 ANOVA (0) | 2020.01.11 |