2020. 1. 15. 16:45ㆍstats
SNUON 통계학
선형회귀분석
1. 직선적합, 잔차, 상관관계
2. 최소제곱추정법
3. 이상점
4. 회귀분석의 추론
17-1. 회귀분석모형의 적합
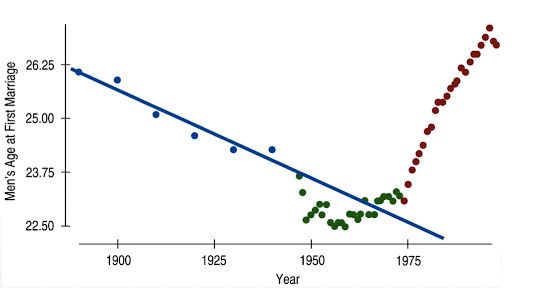
Extrapolation
- 주어진 자료의 범위 밖에서 모형을 이용하여 예측하는 것을 외삽(extrapolation)이라고 한다
- 절편이 외삽에 해당하는 경우가 종종 있다
Examples of Extrapolation
Conditions for the least square line
1) 선형관계 (Linearity)
2) 정규분포 (Nearly normal residuals)
3) 등분산성 (Constant variability)
Conditions (1) Linearity
- 반응변수와 설명변수의 관계는 선형이어야 한다
- 반응변수와 설명변수의 관계가 비선형인 경우 nonparametric regression을 사용하면 된다
- 관계의 선형 여부 파악 방법 : Check using a scatterplot of the data, or a residuals plot

Anatomy of a residuals plot
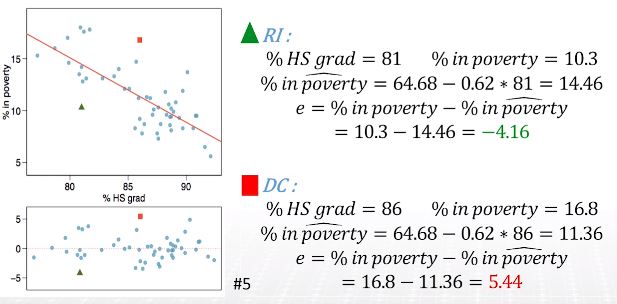
Conditions (2) Nearly normal residuals
- 잔차는 정규분포를 따라야 한다
- 이상점이 있을 경우 혹은 3번째 가정(등분산성)을 만족하지 않을 경우 정규분포를 따르지 않을 수 있다
- 정규분포 따르는지 파악 방법 : 잔차의 histogram 혹은 normal probability plot을 이용하여 check한다 (심각하지만 않으면 OK)
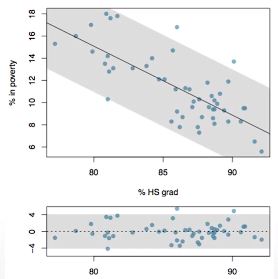
Conditions (3) Constant variability
- 회귀직선 주위의 point의 variability는 일정해야 한다
- 즉 잔차의 분산은 x의 값에 관계없이 일정해야 한다
- 등분산성을 다른 용어로 homoscedasticity
- 등분산성 여부 파악 방법 : residual plot 이용
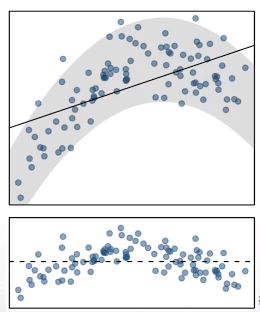
Checking conditions
다음 그림은 회귀분석에서 어떤 가정을 만족하지 않는가?
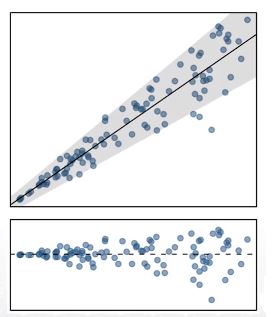
R^2 (R-square)
- 선형모형의 적합정도를 나타내는 정도
- R^2 는 상관계수의 제곱
- R^2은 모형에 의해 설명된 반응변수의 변동정도
- 모형에 의해서 설명되지 않은 변동은 (1) 모형에 포함되지 않은 설명변수 혹은 (2) 자료 자체의 randomness에 기인한다고 생각할 수 있다
Interpretation of R^2
고교졸업률과 빈곤률 예제에서 R = -0.62, R^2 = 0.38
해석 : 빈곤률의 변동 중 38%가 회귀모형으로 설명된다
Poverty vs. region (east, west)
- 설명변수가 범주형, 반응범주가 연속형 변수인 경우에도 회귀분석 사용 가능
(따라서 앞에서 배운 분산분석들도 회귀분석으로 나타낼 수 있음)
poverty_hat = 11.17 + 0.38 * west
- Explanatory variable : region
- Reference level : east (east=0, west=1)
- Intercept : 동부지역의 평균 빈곤율은 11.17%이다 (설명변수에 0을 넣어 계산)
- Slope : 평균적으로 서부 지역 주의 빈곤율이 동부지역 주에 비해서 0.38% 높다 (설명변수에 1을 넣어 계산)
cf. 분산분석에선 표본평균 비교해서 t-검정 등등을 했는데, 회귀분석에선 기울기가 0인지 아닌지 따짐
→ 그래서 진짜 평균에 통계적으로 유의미한 차이가 있나?
Poverty vs. region (northeast, midwest, west, south)
어느 지역이 기준 지역(reference level)인가?
답 : northeast
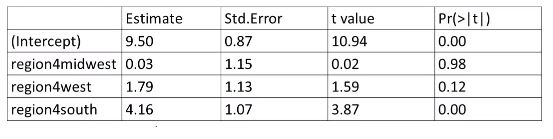
northeast가 기준점
northeast vs. midwest : midwest의 빈곤율이 northeast보다 0.03 높다
northeast vs. west : west의 빈곤율이 northeast보다 1.79 높다
northeast vs. south : south의 빈곤율이 northeast보다 4.16 높다
→ 이들의 차이가 유의미한지에 대한 검정 (t-value)
west vs. south : south의 빈곤율이 west보다 4.16 - 1.79 = 2.37 높다
→ 이들의 차이가 유의미한지에 대한 검정은 나와있지 않음
northeast의 빈곤율이 가장 낮고, south의 빈곤율이 가장 높다
기준점을 south로 바꾸면 estimate의 값은 모두 음수가 될 것이다
17-2. 이상점
Types of outliers

1) 다음 그림에서 이상점(outlier)이 회귀직선에 어떻게 영향을 주었나?
- 왼쪽 하단의 4점을 포함해서 구한 회귀직선과 포함하지 않고 구한 회귀직선이 어떤 모양인지 생각해보자
- 빨간직선은 모든 점을 포함한 경우의 회귀직선이며 왼쪽 하단의 점들을 포함하지 않을 경우 회귀직선의 기울기는 조금 더 낮아질 것이다
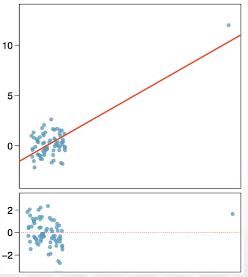
2) 다음 그림에서 이상점은 회귀직선에 어떤 영향을 주었나?
- 이상점이 없다면 반응변수와 설명변수 사이는 큰 연관이 없어 보인다
Some terminology
- Outliers는 대부분의 데이터에서 떨어져 있는 점을 말한다
- Outliers 중 대부분의 데이터에서 수평적으로 떨어져 있는 점을 high leverage points라고 한다
- 회귀직선의 기울기에 영향을 주는 Outliers는 influential points라고 한다
- Outlier가 influential인지 여부를 알아보려면 그 점을 포함한 회귀직선과 포함하지 않은 회귀직선을 그린 후 두 직선의 기울기의 차이를 살펴보면 된다
Influential points
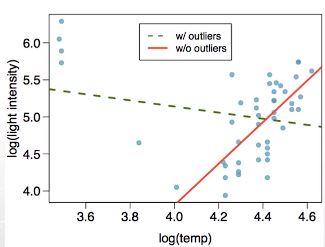
- Outliers 포함하면 음, 포함하지 않으면 양의 상관관계
Types of outliers

1) 다음 그림의 이상점은 어떤 유형?
- High leverage

2) 다음 그림에서 이상점은 기울기에 영향을 미치는가?
- 큰 영향을 미치진 않는다
Recap
다음 중 사실인 것은?
a. Influential points는 항상 회귀직선의 절편을 바꾼다
b. Influential points는 항상 R^2을 축소한다
c. Leverage point가 값이 작을 경우 큰 경우와 비교하여 influential point일 가능성이 더 높다
d. 데이터가 influential point를 포함한 경우 반응변수와 설명변수의 관계는 항상 비선형이다
답: a
Influential points는 기울기를 바꾸므로 절편도 바뀐다 (R^2는 알 수 없음)

Anscombe's quartet

- 4가지 경우의 x 평균/분산, y 평균/분산 모두 같고, 상관계수도 0.816으로 같고, 단순회귀분석도 y = 3 + 0.5x 로 같음
- numerical summary에는 차이가 없지만 시각적으로 확인해보면 매우 다름
- 분석의 첫 단계에는 히스토그램 또는 산점도로 시각화하기! 이후 추론하기
'stats' 카테고리의 다른 글
| 19. 다중회귀분석 I (0) | 2020.01.15 |
|---|---|
| 18. 회귀분석 III (0) | 2020.01.15 |
| 16. 회귀분석 I (0) | 2020.01.15 |
| 15. 모비율에 관한 추론 II (0) | 2020.01.14 |
| 14. 모비율에 관한 추론 I (0) | 2020.01.12 |